Вспомним: В прямоугольном треугольнике высота, проведенная из прямого угла, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу. Следовательно, наша задача построить прямоугольный треугольник с высотой, которая делит гипотенузу на отрезки 3 см и 4 см.
Построение: На произвольной прямой чертим отрезок АН=3 см, продлеваем его на НВ=4 см.
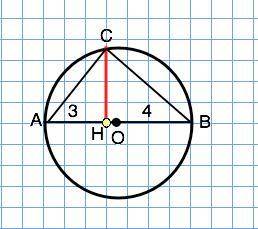
Отрезок АВ равен сумме заданных отрезков. Общепринятым методом делим АВ пополам, середину обозначим т.О. Циркулем чертим из О, как из центра, окружность радиуса АО=ОВ. Из т.Н возводим перпендикуляр. Точку его пересечения с окружностью отметим С. Треугольник АВС - прямоугольный ( т.к. вписанный угол АСВ=90°, т.к. опирается на диаметр построенной окружности), его высота СН - среднее пропорциональное отрезков АН=3 см и ВН=4 см, (Из подобия треугольников АСН и ВСН следует отношение СН:АН=ВН:СН⇒ СН²=АН•ВН)
Объяснение: Каныш Имантаевич Сатпаев принадлежал к плеяде замечательных геологов нашей страны, являлся одним из наиболее выдающихся ученых в области геологии. Он внес громадный вклад в развитие геологической теории, и его исследования привели к открытию богатейших природных ресурсов Казахстана.