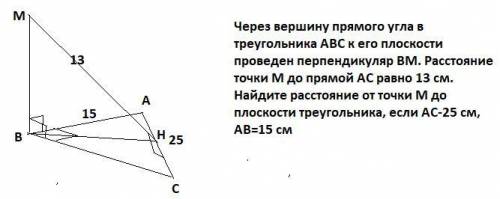
Через вершину прямого угла в треугольника АВС к его плоскости проведен перпендикуляр BM. Расстояние точки М до прямой АС равно 13 см. Найдите расстояние от точки М до плоскости треугольника, если АС-25 см, AB=15 см
Объяснение:
1)Расстоянием от точки до плоскости есть длина перпендикуляра к плоскости -отрезок ВМ .
Расстоянием от точки до прямой является перпендикуляр от точки до прямой. Пусть MH⊥AC , тогда ВН⊥АС по т. о трех перпендикулярах.
2) ΔВМН-прямоугольный , по т. Пифагора , ВМ=√(МН²-ВН²) . Необходимо найти ВН.
3) Найдем предварительно АН (*) : ВА²=АН*АС ⇒ 225=АН*25 ,
АН=9 см
3)ΔВАН -прямоугольный ВН=√(15²-9²)=12( см)
4) ВМ=√(13²-12²)=5 ( см)
===========================
(*)Свойства катетов прямоугольного треугольника: Квадрат катета равен произведению его проекции на гипотенузу.
Пусть высота трапеции х
Проведем параллельно боковой стороне прямую. Она отсечет от трапеции прямоугольный равнобедренный треугольник с углами при основании 45 градусов, половина основания которого равна высоте и меньшему основанию.
Тогда большее основание 2х+4
Полусумма оснований
(2х+4+4):2=(2х+8):2=х+4
Площадь трапеции
х(х+4)=117
х²+4х-117=0 Решим это уравнение:
D = b² - 4ac = 484
√D = 22
х1=9
х2= -13 (не подходит)
Боковую сторону по свойству диагонали квадрата и гипотенузы равнобедренного прямоугольного треугольника найдем по формуле
а√2
Она равна 9√2 см