Треугольник АВС имеет плоскость оси, параллельную стенке АВ. Плоскость пересекает стенки АС и ВС треугольника в точках А1 и В1 соответственно. Найдите отрезок А1С, если АС=15см, А1В1=4см, АВ=20см ОЧЕНЬ
Пусть M- cередина АС, N - середина АВ. Продолжим ВМ на расстояние ВМ, получим Q, продолжим CN на расстояние CN, получим Р. Рассмотрим четырехугольник APBC, в нем диагонали РС и АВ точкой пересечения N делятся пополам, значит, это параллелограмм (признак такой), значит АР параллельна ВС (определение параллелограмма). Рассмотрим четырехугольник ABCQ, в нем диагонали AС и ВQ точкой пересечения M делятся пополам, значит, это параллелограмм (признак такой), значит АQ параллельна ВС (определение параллелограмма). Итак, в точке А проведены две прямые АР и АQ, параллельные ВС. По 5 постулату Евклида (аксиома параллельности) через точку вне прямой можно провести единственную прямую, параллельную данной, значит, точки А, Р, Q лежат на одной прямой
ответ: 32
Объяснение:
Противоположные углы равны, так что один угол 150, а второй 180-150 = 30 градусов.
Напротив угла 30 градусов лежит половина гипотенузы в прямоугольном треугольнике. Опустим высоту из точки B, например.
Получается бок сторона параллелограмма (8см) будет гипотенузой, а высота будет равна 8см / 2 = 4 см, т.к. напротив угла 30 градусов.
Можем найти второй катет по теореме Пифагора: x =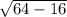 = 4
= 4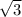 см
см
(но нам он не нужен)
Для нахождения площади параллелограмма нужно высоту умножить на бОльшую сторону)
8*4 = 32 см^2