Объяснение:
1.
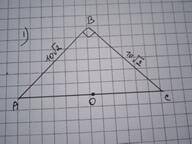
Дано: ΔАВС - прямокутний, ∠В=90°, АВ=ВС=10√2. R - ? r - ?
АС²=АВ²+ВС²=(10√2)² + (10√2)² = 200+200=400; АС=20.
Центр описаного кола припадає на середину гіпотенузи, отже
R=АО=ОС=20:2=10 од.
r=(a+b-c)/2=(10√2 + 10√2 - 20)\2 = (20√2 - 20)/2 = (20√2 - 1)/2 = 10√2 - 1 од.
2.
Катети трикутника а, в, гіпотенуза с. Тоді за умовою
а+в+с=24; а²+в²+с²=200; а²+в²=200-с², за теоремою Піфагора а²+в²=с²
200-с²=с²; 200=2с²; с²=100; с=10 см.
а+в+10=24; а+в=24-10=14 см.
Нехай а=х, тоді в=14-х.
х²+(14-х)²=10²
х²+196-28х+х²-100=0
2х²-28х+96=0
х²-14х+48=0
х=8 та х=6
а=8 см; в=6 см
S=1/2 * 8 * 6 = 24 cм².
ответ: S=54 см², h=7.2 см.
Объяснение: Задачу можно решить разными
и самый простой),
Обозначим треугольник АВС. Отношение его сторон 9:12:15= 3:4:5 - это отношение сторон так называемого «египетского» треугольника. Он прямоугольный. ⇒
Ѕ(АВС)=АВ•ВС:2=9•12:2=54 см²
Наименьшая высота ВН - высота к наибольшей стороне.
ВН=2Ѕ:АС=108:15=7,2 см
Площадь определяется по формуле Герона:
S=√[p•(p-a)(p-b)(p-c)]
p=(a+b+c):2=(9+12+15):2=18
S=√(18•9•6•3)=54 (см²)
для этой конкретной задачи он без особой необходимости, но знать его полезно, нередко применим в других задачах).
Примем отрезок АН=х. ⇒ СН=15-х.
В прямоугольных треугольниках АВН и СВН ВН - общий катет.
Из ∆ АВН по т.Пифагора ВН²=81-х²
Из ∆ СВН по т.Пифагора ВН²=144-225+30х-х² .
Приравняв уравнения квадрата высоты, произведя нужные вычисления, получим х=5,4
⇒ ВН=√(9²-5,4²)=7,2 см .
Ѕ=ВН•АС:2=7,2•15:2=54 см²