
Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
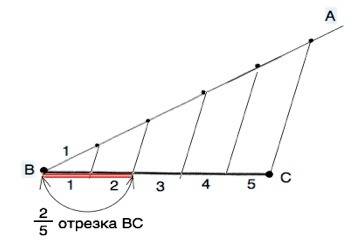
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
25см
Объяснение:
Дано:
SABCD- пирамида.
ABCD- квадрат.
SO=20 см
BD=30см
SD=?
Решение.
ВО=ВD:2=30:2=15см половина диагонали квадрата.
∆SOD- прямоугольный треугольник.
SO и OD катеты.
SD- гипотенуза.
По теореме Пифагора найдем гипотенузу.
SD=√(SO³+OD²)=√(20²+15²)=√(400+225)=
=√625=25 см боковое ребро пирамиды.