площадь трапеции равна 63cos31° +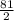 
sin62° , что приблизительно равно 89.76
Объяснение:
Достроим рисунок высотами BE и CF.
Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE
∠ABC=∠CBD=121° , ∠EBC=90° значит ∠ABE=31°
В прямоугольном треугольнике ABE
sin∠ABE=AE/AB ⇒ sin31°=AE/9 ⇒ AE=9*sin31°
cos∠ABE=BE/AB ⇒ cos31°=BE/9 ⇒ BE=9*cos31°
Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =
= 63cos31° + 81sin31°cos31° = 63cos31° + 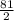sin62° ≈ 89.76
1) АВ=(0;6)
ВС=(-5;-4)
АС=(3;2)
2) Каждая высота делит каждую сторону пополам, значит М=(4+(-5);6+(-4))=(-1;-2), =>
АМ=координаты точки А+координаты точки М=(3;4). По такому же принципу найдешь другие выстоты, сложишь все координаты и разделишь х и у на 3, т.к. высоты 3.