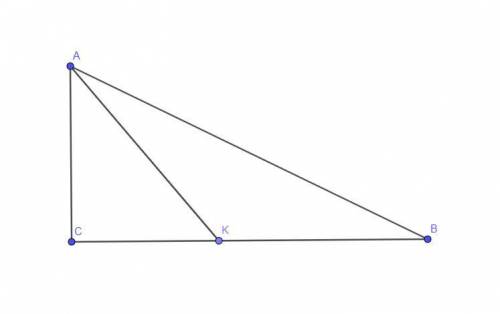
Угол C = 90 градусов.
Угол AKC = 60 градусов
KC = 4 см
Если угол AKC = 60 градусов, то из Теоремы о Сумме Углов треугольника найдем угол CAK:
CAK = 180 - (90+60) = 30 градусам.
Треугольник CAK - прямоугольный.
По свойству прямоугольного треугольника, напротив угла в 30 градусов (угла CAK), лежит катет равный 1/2 от гипотенузы.
т.е AK = CK * 2 = 8 см.
Если угол A равен 60 градусов, а угол CAK = 30 градусов, то угол KAB треугольника AKB равен 60 градусов - угол CAK = 60 - 30 = 30 градусов.
Угол AKB = 180 градусов - угол AKC (по теореме о смежных углах) = 180 - 60 = 120 градусов.
Угол KBA треугольника AKB по теореме о сумме углов треугольника, равен:
180 - (KAB + AKB) = 180 - (120 + 30) = 30 градусам.
У треугольника AKB углы при основании равны м-у собой.
По этому признаку его можно считать равнобедренным.
Его боковые стороны равны:
AK=KB=8 см.
Сторона треугольника BK равна 8 см.
Проекции катетов на гипотенузу - отрезки гипотенузы, полученные в результате проведения высоты к гипотенузе.
Проще говоря, проведи высоту к гипотенузе. Отрезки, на которые поделила эта высота гипотенузу и будут проекциями катетов на гипотенузу.
Итак, высота прямоугольного треугольника, проведённая к гипотенузе равна квадратному корню из произведения проекций катетов на гипотенузу.
Высота, проведённая к гипотенузе (проведённая из вершины прямого угла =
\sqrt{2 cm*8cm} =\sqrt{16 cm^{2} } = 4 cm
2cm∗8cm
=
16cm
2
=4cm
ответ: 4 см.
(Если что-то не понятно, то спрашивайте.)

сторона равна 10 а половина диагонили равна 6
рассмотрим треугольник образованный половинами диагоналей и стороной в 10 см
по теореме пифагора найдём половину неизвестной на диагонали
10*10=6*6+x*x
x-половина неизвестной диагонали
100-36=X*X
X=8
неизвестная диагональ равна 8*2=16
сумма диагоналей равна 16+10=26