Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою 
і проекцією цього катета на гіпотенузу:
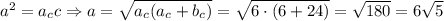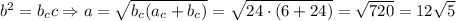см
см
Площа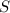 
прямокутного трикутника знаходится як півдобуток його катетів:
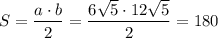см²
Другий б
Висота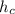 
прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
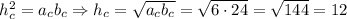см
Площа 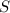будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти 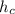, що до неї проведена:
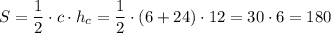см²
Відповідь: 180 см².
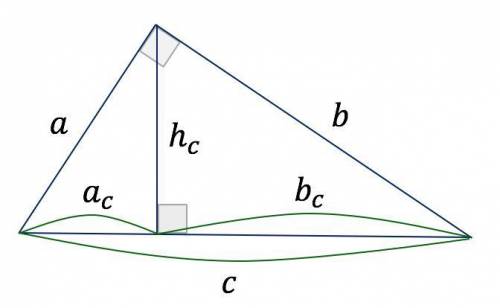
Т.к. АС диаметр, то вписанные углы АВС и АDC, которые на него опираются равны 180:2=90град.
Треугольники АВО и ADО равносторонние, их стороны равны радиусу, значит и углы равны 180:3=60град., следовательно углы BAO и DAO равны 60град., т.е. угол BAD равен 60·2=120град. Угол BСD=180-120=60град. (Сумма углов четырёхугольника равна 360град.)
Углы BCA и DCA равны по 30град. (90-60=30 свойство углов прямоугольного треугольника) и являются вписанными в окружность, следовательно дуги на которые они опираются AB и AD равны 30·2=60град.
Дуги BC и CD так же в 2 раза больше вписанных углов BAC и DAC, которые на них опираются, т.е. 60·2=120град.
ответ: Углы четырёхугольника ABCD равны 120; 90; 60; 90 град. Дуги АВ и CD - 60град., дуги BC CD по 120град.
Р=(2см + 20 см)•2этот будеть