В основании пирамиды SABCD лежит параллелограмм ABCD с центром O. Точка M лежит на отрезке SO, причём OM:MS =1:3.
а) Постройте сечение пирамиды плоскостью, проходящей через
прямую AM параллельно прямой BD.
б) В каком отношении плоскость сечения делит ребро SC?
Объяснение:
а)Проведем через М прямую В₁D₁║ВD .
«Если заданная прямая a, не лежащая в плоскости α, параллельна прямой b, которая принадлежит плоскости α, тогда прямая a параллельна плоскости α.»
Получим точки В₁ и D₁. В плоскости ( АСS) продолжим прямую АМ до пересечения с SC. Соединим В₁-Р и D₁-Р .Полученное сечение искомое.
б)В равнобедренном ΔАСS( т.к пирамида правильная) , высота SO-является медианой. По т. Менелая
СР/РS*(SM/OM)*(AO/AC)=1,
СР/РS*(3/1)*(AO/2AO)=1,
СР/РS*(3/1)*(1/2)=1,
СР/РS=2/3
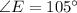
Объяснение:Проведём биссектрисы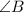
и 
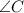. Пусть они пересекаются в точке 
.
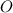Также проведём отрезки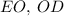
и 
.
========================================
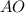Рассмотрим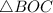
:
Сумма внутренних углов треугольника равна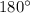
.
========================================
Рассмотрим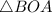
и 
:
========================================
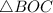Рассмотрим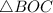
и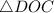 
:
========================================
========================================
Рассмотрим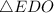
:
========================================
Рассмотрим геометрическую фигуру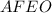
:
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна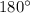
.
Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.
У параллелограмма противоположные углы равны.
========================================