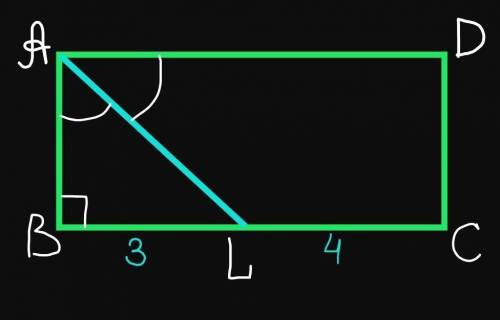
Дано:
ABCD – прямоугольник;
АL – биссектриса угла BAD;
ВL=3 см;
LC=4 см.
Найти:
Р(ABCD)
Так как противоположные стороны прямоугольника паралельны, то AD//BC.
Следовательно угол ALB=угол DAL как накрест-лежащие при параллельных прямых AD u BC и секущей AL.
Угол BAL=угол DAL, так как AL – биссектриса угла BAD.
Исходя из найденного: угол ALB=угол BAL.
Тогда ∆ABL – равнобедренный с основанием AL. Следовательно АВ=BL=3 см.
Периметр прямоугольника можно найти по формуле:
Р=2*(а+б), где а и б – смежные стороны.
Тогда Р(АВСD)=2*(AB+BC)=2*(AB+BL+LC)=2*(3+3+4)=2*10=20 см.
ответ: 20 см.
Объяснение:
Вообщем смысл в следующем.
Основная формула объёма цилиндра:
V=πr²*h; πr² - площадь основания цилиндра, h - высота
V=πr²*h , V=π * OB² * OO₁
Треугольник AOB - равнобедренный, так OA=OB как радиусы основания.
OH - это расстояние от центра O до хорды АВ и является высотой-медианой равнобедренного треугольника, и делит сторону АВ пополам под прямым углом.
Дальше, зная высоту ОН=d и НВ (= 1/2 длины хорды АВ) :
(1) по теореме Пифагора (с²=a²+b²) можно найти сторону ОВ как гипотенузу треугольника НОВ:
ОВ²=d²+HB²; ОВ = √(d²+HB²)
(2) Либо через sin угла α (который ∠АОВ), не зря же нам его величину α дали.
sinα - это отношение противолежащего этому углу катета к гипотенузе
[не забываем, что это ∠АОВ = α, а ∠АОВ = α/2 или =1/2α
то есть sin(1/2α) = НВ/ОВ, отсюда чтобы найти радиус ОВ = НВ / (1/2α).
Высота цилиндра и радиус основания образуют другой прямоугольный треугольник O₁ВО, в котором ∠O - прямой (+90°), ∠В = φ
Зная расстояние от верхнего центра до конца хорды O₁В и радиус ОВ (=r), можно найти высоту O₁О, опять же либо по теореме Пифагора, либо через косинус данного угла ∠O₁ОО = φ.
cosφ - отношение прилежащего катета к гипотенузе, то есть
cosφ = O₁О / O₁В, отсюда высота O₁О = O₁В * cosφ
Таким образом, вычислив радиус ОВ основания цилиндра и высоту O₁О цилиндра, сможем найти его объём по формуле: V=πr²*h
Для выпуклого n-угольника сумма углов равна 180°(n-2).
Доказательство.
Для доказательства теоремы о сумме углов выпуклого многоугольника воспользуемся уже доказанной теоремой о том, что сумма углов треугольника равна 180 градусам.
Пусть A 1 A 2... A n – данный выпуклый многоугольник, и n > 3. Проведем все диагонали многоугольника из вершины A 1. Они разбивают его на n – 2 треугольника: Δ A 1 A 2 A 3, Δ A 1 A 3 A 4, ... , Δ A 1 A n – 1 A n . Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов каждого треугольника равна 180°, а число треугольников – ( n – 2). Поэтому сумма углов выпуклого n -угольника A 1 A 2... A n равна 180° ( n – 2).