0А=6см
Перпендикуляр и наклонные к
плосксти.
Объяснение:
Дано:
SA, SB - наклонные к
плоскости а
SO - перпендикуляр к а
SB=17см
ОВ=15см
SA=10см
------------------------------------
ОА - ?
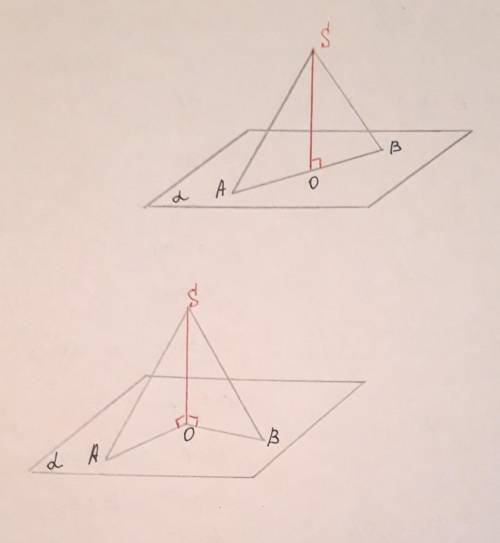
SO - перпендикуляр к плос
кости а ==> SO перпендику
лярна прямым ОВ иОА.
Возможны 2 варианта:
1) точки SAОB лежат в одной
плоскости;
2) точки SAОB не лежат в од
ной плоскости.
Решение и ответ одинаковы
для обоих вариантов.
Рассмотрим треугольник SOB:
<SOB=90°
Треуг. SOB - прямоугольный.
По теореме Пифагора:
SO^2=SB^2-OB^2
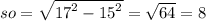
Рассмотрим треугольник SOA:
<SOB=90°
Треуг. SOA - прямоугольный.
По теореие Пифагора:
OA^2=SA^2-SO^2
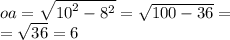
Oтвет:
ОА=6см

Рассмотрим внешние получившиеся треугольники. Они будут все равны между собой по двум сторонам и углу между ними
Угол между сторонами - это угол начального правильного пятиугольникам. а раз начальный пятиугольник правильный, то все его углы равны. Каждая сторона, прилегающая к этому углу равна половине длины стороны начального правильного пятиугольника. Значит, все эти стороны тоже равны между собой. Получается, что все внешние треугольники равны. У равных треугольников равны соответствующие элементы. в данном случае нас интересуют их третьи стороны - те, что образовали новый пятиугольник. раз они равны, то пятиугольник прявильный, чтд
Чертеж то несложный, просто пятиугольник и внутри еще один
1) C = 2*6 см*π = 12 см*π - длина всей окружности.
2) (12 см*π)*2/3 = 8 см*π - длина дуги.
ответ: г) 8 см*π.