
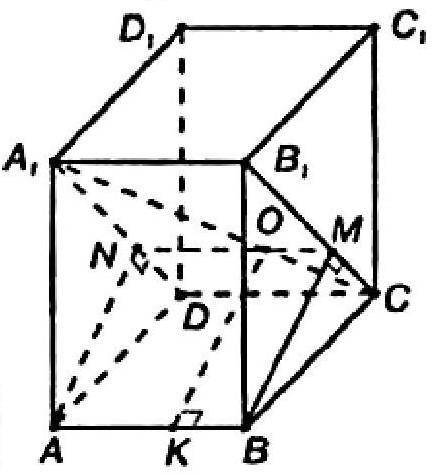
Дано:
ABCDA₁B₁C₁D₁ - правильная четырехугольная призма
BC = 15 см
BB₁ = 20 см
-------------------------------------------------------------------------------------
Найти:
OK - ?
Проведем плоскость А₁В₁СD, а через ребро АВ проведем плоскость ABMN, перпендикулярную плоскости A₁B₁CD.
Так как АВ перпендикулярна боковым граням, то ABMN - прямоугольник.
Пусть О — точка пересечения АС и MN. Проведем ОК⊥АВ. Тогда ОК = ВМ.
Так как ΔВВ₁С - прямоугольный (∠B₁BC = 90°), тогда используется во теореме Пифагора:
B₁C² = BB₁² + BC² ⇒ B₁C = √BB₁² + BC² - теорема Пифагора
B₁C = √(20 см)² + (15 см)² = √400 см² + 225 см² = √625 см² = 25 см
Далее мы находим площадь ΔВВ₁С по формуле Герона:
S(ΔВВ₁С) = √p(p-BC)(p-BB₁)(p-B₁C) - Формула Герона
p = BC+BB₁+B₁C/2 = 15 см + 20 см + 25 см / 2 = 60 см/2 = 30 см
S(ΔВВ₁С) = √30 см × (30 см - 15 см)×(30 см - 20 см)×(30 см - 25 см) = √30 см × 15 см × 10 см × 5 см = √22500 см⁴ = 150 см²
Далее мы воспользуемся площадью треугольника ВВ₁С по такой формуле:
S(ΔВВ₁С) = 1/2 × B₁C × BM - площадь треугольника
Следовательно по такой формуле мы находим высоту BM:
BM = 2S(ΔВВ₁С)/B₁C = 2×150 см²/25 см = 300 см²/25 см = 12 см ⇒ OK = BM = 12 см
ответ: OK = 12 см
P.S. Рисунок показан внизу↓
Перпендикулярным отрезком, проведенным из точки к данному прямой называют перпендикуляром .
Теорема — утверждение, справедливость которого устанавливается путем рассуждения, а сами рассуждения — доказательством теоремы
Условие — это начало теоремы, а заключение — конец теоремы
Теорема о перпендикуляре , проведенным из точки к данной прямой: из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и притом только один
Медиана треугольника— это отрезок,соединяющий вершину треугольника с серединой противоположной стороны
Любой треугольник имеет три медианы.
Биссектриса треугодиника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны
Любой треугольник имеет три биссектрисы.
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Любой треугольник имеет три высоты.
Равнобедренным треугольником называется треугольник, у которого две его стороны равны.
Стороны равнобедренного треугольника называют боковыми сторонами.
Равносторонний треугольник — это треугольник, у которого все стороны равны.
Свойство : все углы равностороннего треугольника равны.
Теорема об углах равнобедренного треугольника: В равнобедренном треугольнике углы при основании равны.
Теорема о биссектрисе равнобедренного треугольника: в равнобедренном треугольнике биссектриса , проведенная к основнованию, является медианой и высотой.
Теорема о равестве треугольников: 1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и уголу между ними другого треугольника, то такие треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Окружность— геометрическая фигура, состаящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка — центр окружности.
Радиус — отрезок соединяющий центр окружности с какой либо точкой окружности.
Хорда — отрезок соединяющий две точки окружности
Диаметр — хорда проходящая через центр окружности