1. Радиус сферы равен половине диаметра, R = 25 см.
Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен сечению. это и есть расстояние от центра сферы до сечения.
Итак, ОА = 25 см, ОС = 15 см. Из прямоугольного треугольника АОС по теореме Пифагора находим радиус сечения:
АС = √(ОА² - ОС²) = √(25² - 15²) = √(625 - 225) = √400 = 20 cм
Линия пересечения сферы плоскостью - окружность. Ее длина:
C = 2π·AC = 2π · 20 = 40π см
2. Сечение шара - круг. Его площадь равна 36π см²:
Sсеч = π · r² = 36π
r² = 36
r = 6 см
Из прямоугольного треугольника АОС по теореме Пифагора:
ОС = √(ОА² - r²) = √(100 - 36) = √64 = 8 см - искомое расстояние.
3. Радиус большого круга равен радиусу шара.
Площадь сечения:
Sсеч = πr²
Площадь большого круга:
S = πR², R = √(S/π)
Sсеч / S = πr² / (πR²) = r²/ R²
По условию Sсеч / S = 3 / 4, ⇒
r²/ R² = 3 / 4, тогда r/R = √3/2
В прямоугольном треугольнике АОС r/R - это косинус угла А.
Тогда ∠А = 30°.
Расстояние от центра шара до сечения - отрезок ОС. Это катет, лежащий напротив угла в 30°, значит он равен
OC = R/2 = √(S/π) / 2 = √S/(2√π)
4. Радиус шара равен половине диаметра:
R = 2√3 см
Прямоугольный треугольник ОВС равнобедренный, так как в нем острый угол равен 45°, поэтому
ОС = r = R/√2 = 2√3 / √2 = √6 см
Sсеч = πr² = π · (√6)² = 6π см²
а). От 1 до 3 прямых.
б). От 1 до 6 прямых.
в). От 1 до 10 прямых.
г). От 1 до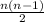
прямых.
Объяснение:
г). [Сначала разберем общий случай] Найдем максимальное количество прямых, которое можно провести через определенные n точек, никакие три из которых не лежат на одной прямой.
Возьмем какую-нибудь точку из n точек. К скольким точкам можно провести из нее прямую? Так как никакие три из n точек не лежат на одной прямой, то всего будет сделать это. Так как это рассуждение можно сделать с любой из n точек, то мы пока получаем всего возможных сделать это: n(n-1) .
Но нужно учесть, что прямая от точки B до точки А - это тоже самое, что и прямая от точки А до точки В. Поэтому общее количество нужно разделить на 2:
При этом можно провести любое натуральное (0 прямых не считается) число прямых меньше указанного выше числа.
а). Через три точки максимум можно провести:
б). Для четырех точек:
То есть, прямых можно провести любое число от 1 до 6.
в). Для пяти точек максимум равен:
То есть, прямых можно провести любое число от 1 до 10.
То есть всего можно провести 1 прямую, 2 и 3 прямые.
Примечание:
В решении мы пользовались, тем, никакие ТРИ из прямых не лежат на одной прямой (фотография 2).