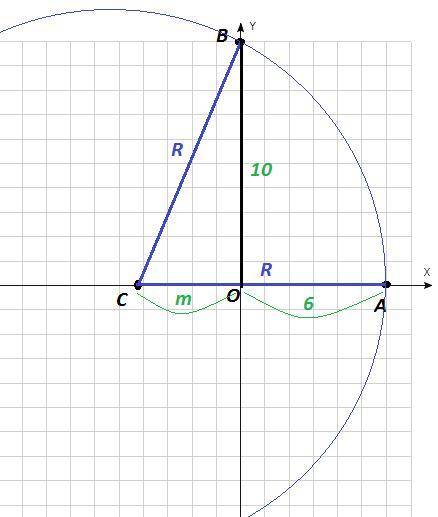
Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64; 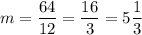
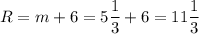
Общее уравнение окружности с центром в точке С и радиусом R
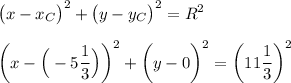
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
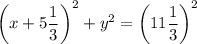
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
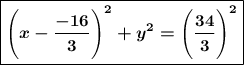
Объяснение:
координаты вектора вычисляются так: из соответствующей координаты конца вектора нужно вычесть соответствующую координату начала вектора.
получим координаты вершин параллелограмма, выраженные через координаты одной точки (точки А, например)
координаты векторов-диагоналей параллелограмма вычисляются аналогично...
косинус угла между векторами = частному от деления скалярного произведения векторов на произведение длин векторов.
скалярное произведение векторов=сумме произведений соответствующих координат.
длина вектора=корню квадратному из суммы квадратов координат (т.Пифагора)