Объяснение:
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла[2], т.е. как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому исследование его свойств проводилось начиная с глубокой древности.
Понятие треугольника допускает различные обобщения. Можно определить это понятие в неевклидовой геометрии (например, на сфере): на таких поверхностях треугольник определяется как три точки, соединённые геодезическими линиями. В {\displaystyle n}n-мерной геометрии аналогом треугольника является {\displaystyle n}n-й мерный симплекс.
Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.
1)Диагональ квадрата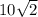
2)Такого правильного многоугольника не существует
3)Периметр ромба 60
Объяснение:
1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ =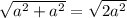
=
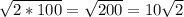, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =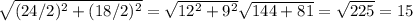
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
= 4 * 15 = 60