правильная пирамида - все углы равны и стороны равны..т.е. все углы по 60 градусов и все стороны по 3 см..отсюда и считайся площадь по формуле площади треугольника.
У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть 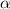 - острый угол,
- острый угол, 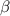 - тупой. Тогда имеет место соотношение
- тупой. Тогда имеет место соотношение
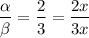
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
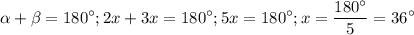
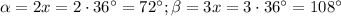
ответ: 72°, 72°, 108°, 108°
Условие слегка непонятное - я буду считать, что все грани пирамиды - правильные треугольники. То есть под плоским углом при вершине я буду понимать угол между двумя ребрами. Таким образом, задан тетраэдр.Основанием считается "нижняя" грань, на самом деле все грани одинаковы, но "по привычке" называем основанием то, что внизу, а высотой - высоту, перпендикулярную именно "основанию".
Пусть боковая сторона равна а.
Рассмотрим прямоугольный треугольник, образованный боковой стороной тетраэдра, её проекцией на основание и высотой пирамиды. Ясно, что основание высоты равноудалено от вершин основания, то есть проекция бокового ребра на основание есть радиус R описанной окружности вокруг треугольника со стороной а, то есть R = а*√3/3; (это просто - R = 2/3 от высоты правильного треугольника, а высота равна h = а*sin(60) = a*√3/2; не путать это с высотой пирамиды!).
Заданный отрезок длины 3 является в построенном прямоугольном треугольнике МЕДИАНОЙ, то есть равен половине гипотенузы. А роль гипотенузы играет боковое ребро. Поэтому а = 6 :))
Площадь правильного треугольника со стороной 6 равна a*h/2 = 6^2*√3/4; а всего у нас 4 одинаковых грани, то есть площадь всей поверхности пирамиды равна
36*√3