Площадь правильного треугольника находят по формуле:S=1/2*a*h, где а - это основание, а h -высота, опущенная на основание
У нас известна а , т.к. все стороны правильного треугольника равны⇒ а=6 см.
Найти высоту можно по формуле Пифагора.
Так, высота в равностороннем треугольнике (правильный треугольник - это равносторонний треугольник) является также биссектрисой и медианой.
Как медиана, она делит сторону, на которую опущена, пополам. Проведя высоту получаем прямоугольный треугольник, один из катетов которого есть высотой правильного треугольника, а второй из катетов равен половине стороны: 6:2=3 (см).
Находим ее (высоты правильного треугольника) значение : 6²+3²=36+9=45, √45=√9*5=3√5 (см),
тогда площадь правильного треугольника равна: 1/2*6*3√5=9√5 (см)
Пусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEF
СD= 8см
Объяснение:
Высота к основанию равнобедренного треугольника является и медианой. Следовательно АD=DB=AB:2.
РABC=АВ+ВС+АС= 2BC+AB (1)
PACD=СD+ВС+AD= CD+BC+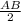 (2)
(2)
2ВС+АВ=31,6(3 ) _ получилось из (1) подставили цифры
Домножим второе у-е на 2 и заменим подчёркнутое на (3) и цифры
2PACD=2СD+2ВС+АВ;
2*23,8=2СD+31,6;
2СD=47,6-31,6;
CD=16:2
СD=8(см)