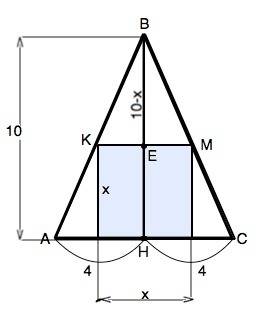
Сделаем схематический рисунок осевого сечения данной фигуры.
Получим равнобедренный треугольник с вписанным в него квадратом.
Примем сторону квадрата (высоту и диаметр цилиндра) равной х.
Тогда верхний диаметр цилиндра КМ=х будет основанием равнобедренного треугольника КВМ. Оно параллельно диаметру конуса.
Диаметр конуса =2•4=8
Высота ∆ КВМ=10
Треугольники АВС и КВМ подобны по равным углам при основаниях и общему углу В.
Из подобия следует отношение:
АС:КМ=ВН:ВЕ
8:х=10:(10-х)
18х=80
х=40/9
V=πr²•h
Радиус цилиндра r= x:2=20/9
Высота цилиндра h=40/9
V=(π•400•40):81•9= ≈ 65,36 (ед. объема)
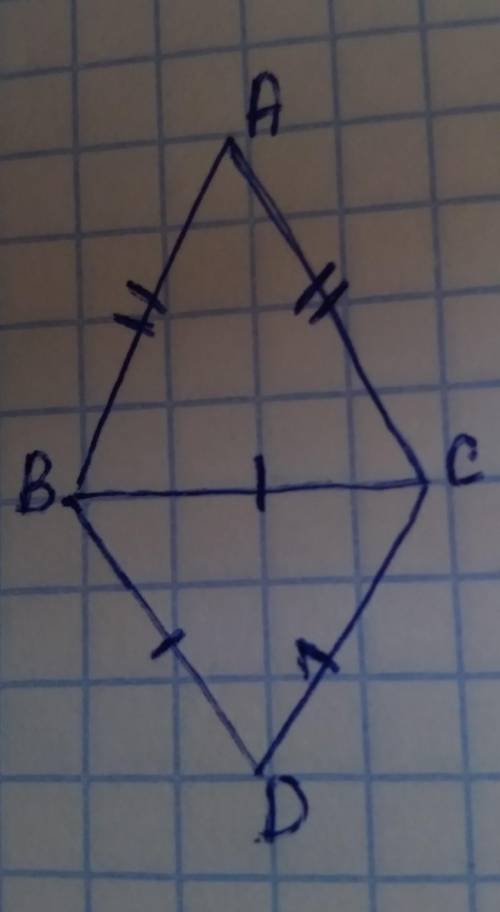
Периметр - это сумма всех сторон в треугольнике, тогда:
AB + AC + BC = 55 см
BC + BD + CD = 51 см
С условия AB = AC, тогда:
2AB + BC = 55 см
Так, как треугольник равносторонний:
3BC = 51 см
Решим систему уравнений:
BC = 55 - 2AB ⇒
3 (55 - 2AB) = 51 ⇒
160 - 6AB = 51 ⇒
-6AB = -144 ⇒
AB = 19 см ⇒
Тогда:
BC = 55 - 2 · 19 = 17 см
ответ: 19 и 17 сантиметров.