
Искомая площадь - сумма площадей двух сегментов круга, отсекаемых от него ромбом.
Угол СТО опирается на диаметр и равен 90º
Расстояние от точки до прямой - длина отрезка из этой точки, перпендикулярного к этой прямой.
ОТ ⊥ ВС и является расстоянием от О до ВС.
ТО=3 см ( расстояние от точки до прямой - перпендикуляр)
Формула площади сегмента ромба:
S=0,5R²[(πα/180º)-sin α],
где R радиус круга, α - угол сегмента в градусах, π≈3,14
∆ ВОС~∆ ВОТ ( прямоугольные с общим углом при В)
∠ВОТ=∠ВСО
tg∠ВОТ=ВТ:ТО=√3:3=1/√3. Это тангенс 30º
∆ ТО1С равнобедренный.
∠ ТСО₁=∠ СТО₁
∠ ТО₁С=180-2∠ТСО₁
Отсюда ∠ТО₁С=180º-2*30º=120º
Из ∆ ТОС
ОС=ТО:sin30º=3:0,5=6 см
R=ОС:2=3 см
Сумма площадей 2-х сегментов
S=R²[(πα/180º)-sin α],
sin 120º=√3/2
Подставим найденные величины:
S=3²[(π120º/180º)-√3/2]
S=6π-9√3)/2
S=6π-4,5√3≈11,055 см²
-------
В приложении решение дано несколько иное, хотя принцип тот же.
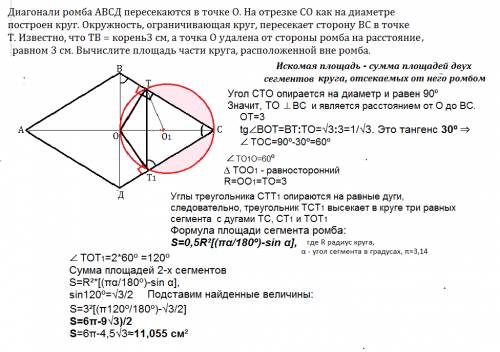
решение написано не по порядку
Объяснение:
3). По свойству вертикальных углов угол COD будет равен углу ВОА, по 2 признаку равенства треугольников (когда равны два угла и сторона, прилежащая к ним) треугольники OCD и OBA будут равны, следовательно будут равны и их стороны BO = CO, AB = CD, AO = OD
если OD = AO значит треугольник AOD будет равнобедренный
2). 21 см или 24 см
так как треугольник равнобедренный, то его две стороны будут одинаковыми
тогда 6*2+9 = 21 или 9*2+6 = 24
1) по свойству вертикальных углов угол ROS = углу POT следовательно треугольники будут равны по 1 признаку равенства треугольников (по двум сторонам и углу между ними)