Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности.
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π.
Сумма градусных мер двух дуг окружности с общими концами равна 360º.
Часть плоскости, ограниченная окружностью, называется кругом.
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора.
Две окружности, имеющие общий центр, называются концентрическими.
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Следствие 1.Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулыДлина окружности:C = 2∙π∙R
Длина дуги окружности:R = С/(2∙π) = D/2
Диаметр:D = C/π = 2∙R
Длина дуги окружности:l = (π∙R) / 180∙α,
где α — градусная мера длины дуги окружности)
S = π∙R2
Площадь кругового сектора:S = ((π∙R2) / 360)∙α
Уравнение окружностиВ прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (xо;yо) имеет вид:(x - xо)2 + (y - yо)2 = r2
x2 + y2 = r2
Хорошей учёбы!
ответ: α=arccos(1/9)≈84°.
Объяснение:
Пусть α - искомый угол. Пусть s - расстояние от города В до точки, через которую проходит перпендикуляр к шоссе, проведённый из города А. Тогда дина маршрута l=s-54*ctg(α)+54/sin(α). Пусть m - масса груза, тогда стоимость доставки груза S=52*m*[s-54*ctg(α)]+468*m*54/sin(α). Так как m=const и s=const, то задача сводится к нахождению наименьшего значения функции S(α). Находим её производную: S'(α)=[52*54*m-468*54*m*cos(α)]/sin²(α) и приравниваем её к нулю. Отсюда после сокращения на произведение 54*m следует уравнение 52-468*cos(α)=0, откуда cos(α)=52/468=1/9. Тогда α=arccos(1/9)≈84°.
Для решения этой задачи необходимо найти площадь треугольника.
Найдем ее по формуле Герона :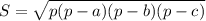
,где p-полупериметр треугольника
В этом случае р=24
Найдем радиус описанной окружности ,т.е. R
Найдем радиус вписанной окр.,т.е. r