
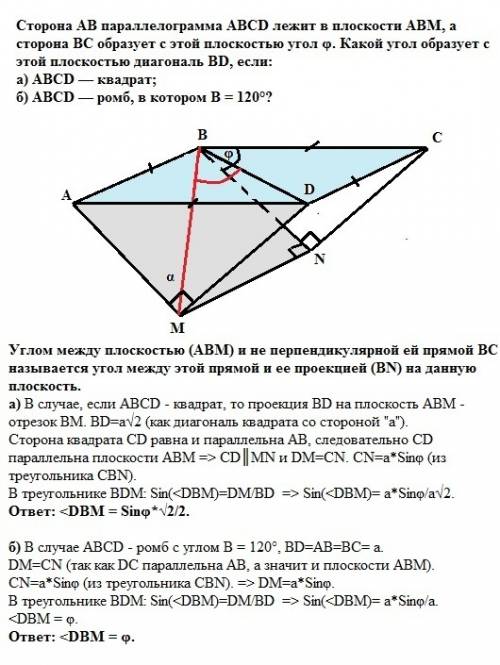
Определение: "Углом между плоскостью (АВМ) и не перпендикулярной ей прямой ВС называется угол между этой прямой и ее проекцией (ВN) на данную плоскость.
а) В случае, если АВСD - квадрат, то проекция ВD на плоскость АВМ - отрезок BM. BD=a√2 (как диагональ квадрата со стороной "а"). Сторона квадрата CD равна и параллельна АВ, следовательно CD параллельна плоскости АВМ => CD║MN и DM=CN. CN=a*Sinφ (из треугольника CBN).
В треугольнике BDM: Sin(<DBM)=DM/BD => Sin(<DBM)= a*Sinφ/a√2.
ответ: <DBM = Sinφ*√2/2.
б) В случае АВСD - ромб с углом В = 120°, BD=АВ=BC= а. DM=CN (так как DC параллельна АВ, а значит и плоскости АВМ).
CN=a*Sinφ (из треугольника CBN). => DM=a*Sinφ.
В треугольнике BDM: Sin(<DBM)=DM/BD => Sin(<DBM)= a*Sinφ/a.
ответ: <DBM = φ.
Несмотря на то, что прямоугольный треугольник, сторонами которого являются высота, медиана и отрезок гипотенузы между ними, является Пифагоровым (8, 15,17), и высота делит гипотенузу, длина которой равна 17*2 = 34, на отрезки длиной 17 - 8 = 9 и 17 + 8 = 25 (как и положено, 9*25 = 15^2), сам треугольник не является целочисленным, и его катеты надо просто вычислить по теореме Пифагора.
Меньший катет равен √(9^2 + 15^2) = 3*√34;
Больший катет равен √(25^2 + 15^2) = 5*√34;
Ну да, еще периметр 34 + 8*√34 ;