Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
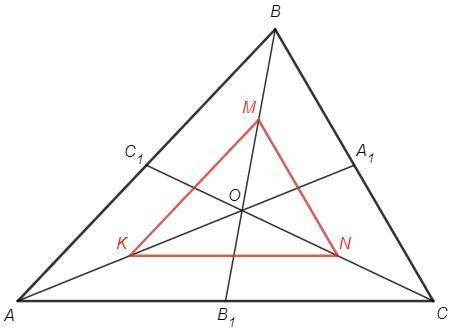
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
есть такое свойство про пересекающиеся в окружности хорды, произведени отрезков одной хорды равно произведению отрезков другой.
АК*KB=CK*KD
AK=8
CK=6
BK=x
KD=35-x
6(35-x)=8x
210-6x=8x
14x=210
x=15
BK=15
KD=35-15=20
2) диаметр окружности равен стороне квадрата
D=8 см
гипотенуза треугольника (с) равна диаметру
с=8см
катет (а), лежащий напротив угла 30 градусов, равен
половине гипотенузы
а=с/2=4 (см)
второй катет (в) можно найти по т Пифагора
в"2=с"2-а"2=64-16=48=16·3; в=4√3
" значок степени
площадь треугольника равна половине произведения катетов
S=(1/2)·4·4√3=8√3
ответ: 8√3 кв см
с(4;9)