теорема. прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
рассмотрим следующий рисунок.
ah - перпендикулярен плоскости α. am это наклонная в плоскости α; a - прямая, проведенная в плоскости α через точку м перпендикулярно к проекции hm наклонной. теперь, докажем, что прямая а перпендикулярна ам. для этого рассмотрим плоскость amh.
по условию прямая а перпендикулярна нм. также прямая а перпендикулярна ан, так как ан перпендикулярна плоскости α. прямые нм и ан принадлежат плоскости анм и пересекаются. из этих трех пунктов следует, что прямая а перпендикулярна плоскости амн, значит, она перпендикулярна любой прямой, которая принадлежит плоскости амн.
так как прямая ам принадлежит плоскости амн, значит прямая a и прямая ам перпендикулярны между собой. что и требовалось доказать.
так как в теореме присутствуют три перпендикуляра, ан, нм и ам, теорема называется теоремой о трех перпендикулярах. все три прямых угла показаны на рисунке, который в начале доказательства. помимо основной теоремы о трех перпендикулярах, существует и обратная теорема о трех перпендикулярах.
обратная теорема
прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
. отрезок ad перпендикулярен к плоскости равнобедренного треугольника авс. известно, что ав = ас = 5см, вс = 6 см, ad = 12 см. найти расстояние от точки а до прямой вс.
решение.
пусть точка е это середина вс. тогда вс будет перпендикулярным ае. то есть ае будет расстояние от точки а до прямой вс.
еа является проекцией de на плоскость авс. ае перпендикулярен вс, а следовательно по теореме о трех перпендикулярах de будет перпендикулярен bc. получаем, что de - это расстояние от точки d до отрезка bc. теперь будем определять ae.
ве = (1/2)*вс = 3 см.
так как треугольник аве прямоугольный, то можем по теореме пифагора найти ае.
ае^2 = ab^2-be^2 = 25-9 = 16, следовательно, ае = 4 см.
ответ. 4 см.
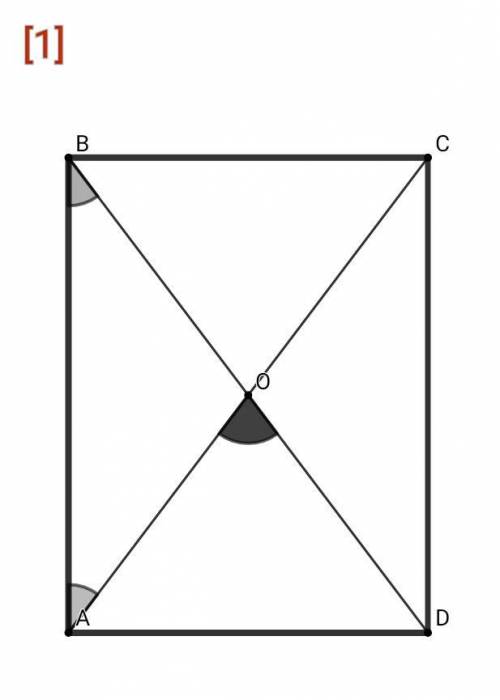
По свойству прямоугольника его диагонали равны и точкой пересечения делятся пополам, при этом образуя две пары равных и равнобедренных треугольников ⇒ АО = СО = ВО = ОD ⇒ ΔAOB - равнобедренный, так как АО = ВО. Углы при основании равнобедренного треугольника равны: ∠АВО = ∠ВАО = 36°
∠АОD = ∠ABO + ∠BAO = 2•∠ABO = 2•36° = 72° - по свойству внешнего угла ∠АОD
ответ: 72°
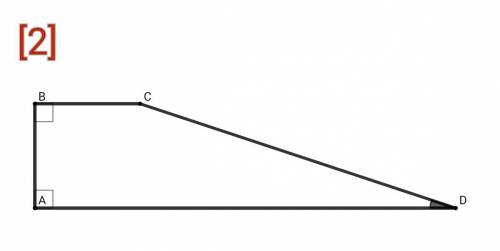
[2]Найдите углы прямоугольной трапеции, если один из углов равен 20°.В прямоугольной трапеции присутствуют два прямых угла при одной боковой стороне, при другой - острый и тупой угол ⇒ ∠ADC = 20°, ∠ABC = 90° , ∠BAD = 90°. Сумма углов в четырёхугольнике составляет 360° ⇒ ∠BCD = 360° - 90° - 90° - 20° = 180° - 20° = 160°
ответ: 20° , 90° , 90° , 160°
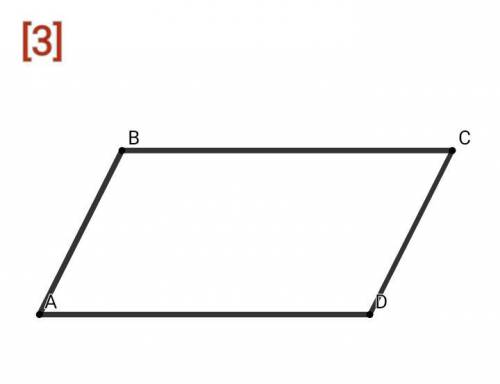
[3]Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.По свойству параллелограмма его противолежащие стороны попарно параллельны и равны ⇒ AB = CD , BC = AD
Пусть AB = x, тогда BC = 2x, составим уравнение:
P (abcd) = 2•(AB + BC)
30 = 2•(x + 2x) ⇒ 6x = 30 ⇒ x = 5 см
Значит, AB = CD = 5 см, BC = AD = 2•5 = 10 см
ответ: 5 см, 10 см, 5 см, 10 см
[4]В равнобедренной трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.По свойству равнобедренной трапеции углы при его основаниях равны ⇒ ∠АВС = ∠BCD , ∠BAD = ∠CDA
По условию ∠BAD + ∠CDA = 96° ⇒ 2•∠BAD = 96° ⇒ ∠BAD = ∠CDA = 48°
Сумма углов в четырёхугольнике составляет 360° ⇒ ∠ABC + ∠BCD = 360° - 48° - 48° ⇒ ∠ABC + ∠BCD = 264° ⇒ 2•∠ABC = 264° ⇒ ∠ABC = ∠BCD = 132°
ответ: 48° , 48° , 132° , 132°
[5]Высота ВМ, проведенная из вершины угла ромба АВСD образует со стороной АВ угол в 30°, АМ = 4 см. Найдите длину диагонали ВD ромба, если точка М лежит на стороне АD.В прямоугольном ΔАВМ: катет, лежащий против угла в 30°, равен половине гипотенузы ⇒ АВ = 2•АМ = 2•4 = 8 см
Сумма углов в треугольнике составляет 180°: ∠ВАМ = 180° - 90° - 30° = 60°
В ромбе все стороны равны: АВ = ВС = CD = AD = 8 см
ΔBAD - равнобедренный, так как AB = AD = 8 см. В равнобедренном треугольнике углы при основании равны: ∠ABD = ∠ADB = (180° - ∠BAD)/2 = (180° - 60°)/2 = 60° ⇒ ∠BAD = ∠ABD = ∠ADB = 60°
Значит, ΔABD - равносторонний, AB = AD = BD = 8 см
ответ: 8 см


ответ во вложении
Объяснение: