1) угол при вершини =180-45-45=90
S=0.5*12.8*12.8=81.92
2)В прямоугольном треугольнике медиана, проведенная к гипотенузе = 1/2 гипотенузы
треугольник АВС, уголА=90, ВС гипотенуза, АН - медиана
АН = а, АВ=4, АС=а+0,5, ВС=2а
АВ в квадрате = ВС в квадрате - АС в квадрате
16= 4а в квадрате - (а+0,5) в квадрате
16 = 4а в квадрате - а в квадрате - а - 0,25
3а в квадрате - а - 16,25 =0
а = (1+- корень(1+ 4 х 3 х 16,25)) / 2 х 3
а= (1 +-14) / 6
а= 2,5 = АН
АС = 2,5+0,5=3
Площадь = 0.5* АВ* АС =0.5* 3* 4 =6
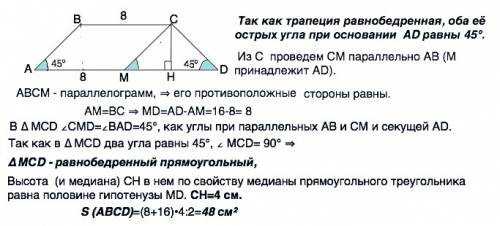
Так как трапеция равнобедренная, оба её острых угла при основании АD равны 45°.
Из С проведем СМ параллельно АВ (М принадлежит АD).
АВСМ - параллелограмм, ⇒ его противоположные стороны равны.
АМ=ВС ⇒ МD=АD-AM=16-8= 8
В ∆ МСD ∠СМD=∠ВАD=45°, как углы при параллельных АВ и СМ и секущей АD.
Так как в ∆ МСD два угла равны 45°, ∠ MCD= 90° ⇒
∆ МСD - равнобедренный прямоугольный,
Высота (и медиана) СН в нем по свойству медианы прямоугольного треугольника равна половине гипотенузы МD. СН=4 см.
S (ABCD)=(8+16)•4:2=48 см²
Треугольник равнобедренный, углы при основании=45, угол при вершине = 180-45-45=90
треугольник прямоугольный, площадь = 1/2 х катет1 х катет2 = 1/2 х 12,8 х 12,8 =81,92
вторую задачу - написано не понятно, напиши понятно
один из катетов больше медианы на 0,5 м, да ладно
В прямоугольном треугольнике медиана, проведенная к гипотенузе = 1/2 гипотенузы
треугольник АВС, уголА=90, ВС гипотенуза, АН - медиана
АН = а, АВ=4, АС=а+0,5, ВС=2а
АВ в квадрате = ВС в квадрате - АС в квадрате
16= 4а в квадрате - (а+0,5) в квадрате
16 = 4а в квадрате - а в квадрате - а - 0,25
3а в квадрате - а - 16,25 =0
а = (1+- корень(1+ 4 х 3 х 16,25)) / 2 х 3
а= (1 +-14) / 6
а= 2,5 = АН
АС = 2,5+0,5=3
Площадь = 1/2 х АВ х АС = 1/2 х 3 х 4 =6