а) 56 кв. см;
б) ... .
Объяснение:
а) Дано:
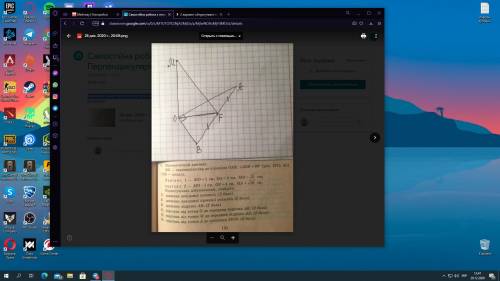
АВСD - р/б трапеция;
АВ=CD=5 см (боковые стороны);
AD и BC - основания ABCD;
АВ=17 см;
ВС=11 см;
BM и CN - высоты АВСD.
Найти: S (ABCD).
1) Рассмотрим прямоугольник (т. к. ВМ и CN - высоты АВСD) МВСN:
ВC=MN=11 см (как противоположные стороны параллелограмма) => АМ=DN=(AD-MN):2= (17 см - 11 см) : 2 = 6 см : 2 = 3 см.2) Рассмотрим прямоугольный треугольник (т. к. ВМ - высота) АВМ:
По теореме Пифагора: высота ВМ^2=АВ^2-АМ^2=5^2-3^2=25-9=16 => ВМ = корень из 16 = 4 см.3) Теперь можем найти площадь трапеции ABCD:
S (ABCD)= 1/2•(AD+BC)•BM= 1/2 • (17 см + 11 см) • 4 см = 1/2 • 28 см • 4 см = 14 см • 4 см = 56 кв. см.ответ: 56 кв. см.
б) Дано:
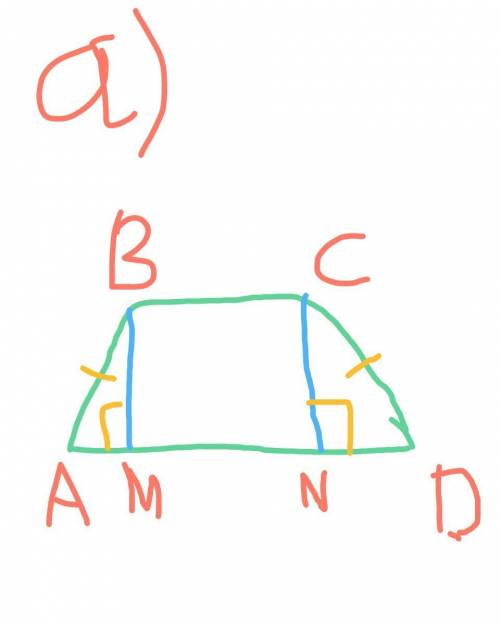
АВСD - р/б трапеция;
АВ=CD (боковые стороны);
AD и BC - основания ABCD;
АВ=8 см;
ВС=2 см;
Угол АDC=60°;
BM и CN - высоты АВСD.
Найти: S (ABCD).
1) ... .
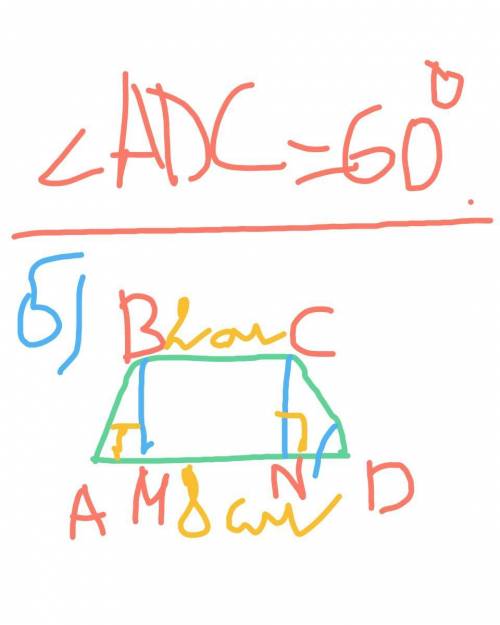
Нехай є трикутна піраміда, сторони основи якої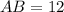
см, 
см,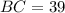 
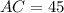см. Якщо всі бічні грані піраміди нахилені до основи під кутом 
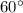, то висота 
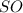піраміди лежить у центрі 
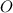вписаного кола, де 
, 
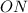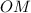та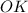 
— радіуси цього кола.
Треба знайти площу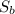
бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
Знайдемо площу основи за формулою Герона:
Знайдемо радіус вписаного кола:
Отже,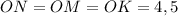
см.
Розглянемо прямокутний трикутник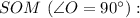
Розглянемо трикутник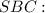
Розглянемо трикутник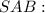
Розглянемо трикутник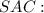
Отже, площею бічної поверхні заданої піраміди буде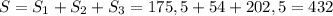
см².
Відповідь: 432 см².