Пирамида усечена плоскостью, параллельной основанию.
Отсеченная пирамида подобна исходной 6:8 =3:4
Следовательно, части, заключенные между плоскостями, относятся к исходным 1:4.
Найдем высоту и апофему исходной пирамиды.
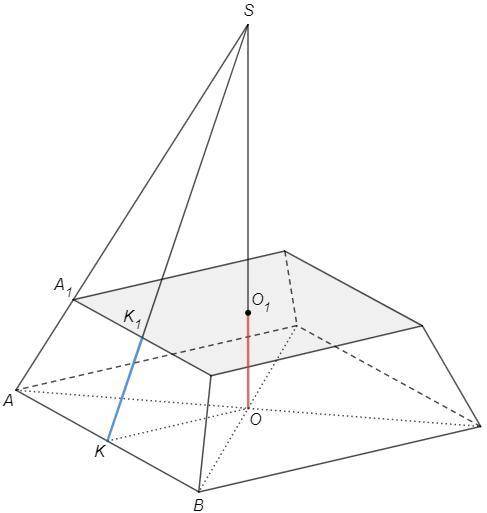
Правильная пирамида, в основании квадрат, вершина падает в центр основания.
Центр описанной окружности квадрата - пересечение диагоналей.
Диагонали квадрата перпендикулярны, равны, точкой пересечения (O) делятся пополам.
AO =AB sin45 =8*√2/2 =4√2
SO⊥(ABC), SAO=60
SO =AO tg60 =4√2*√3 =4√6 (исходная высота)
Боковые грани правильной пирамиды - равнобедренные треугольники.
Высота боковой грани - апофема - является медианой.
K - середина AB, KO=AB/2=4 (медиана из прямого угла)
SK =√(SO^2+KO^2) =4√(1+6) =4√7 (исходная апофема)
OO1/SO =KK1/SK =1/4
высота усеченной пирамиды OO1=√6 (см)
апофема усеченной пирамиды KK1=√7 (см)
прямая CF, параллельна прямой BE, лежащей в плоскости CBE и проходит через точку С этой плоскости. Значит точки B, C, E и F лежат в одной плоскости.
медианы AA1, BB1 параллельны плоскости a. При этом не совпадают и лежат в плоскости треугольника ABC. Значит плоскость треугольника ABC || a.
прямые BС и EF не пересекаются, т.к лежат в параллельных плоскостях ABC и a. При этом они принадлежат одной плоскости BCEF. Значит они параллельны.
итого, B, C, E, F лежат в одной плоскости BC || EF, BE || CF. Значит BCEF - параллелограм
Задача 1
1) Дуга ВС = 2 угла ВАС (т.к. угол вписанный)
Дуга ВС = 126°
2) Дуга ВД = дуге ДQ = дуге QC = 126° : 3 = 42°
3) Дуга ВАС = 360° - 126° = 234°
Проведем вписанный угол ВСМ так, чтобы он был равен 90°, тогда дуга
ВАМ будет равна 180°
Проведем вписанный угол ВАМ так, чтобы он был равен 90°, тогда угол САТ
будет равен 90° - 63° = 27°
Дуга СМ равна 2 угла САМ (т.к. он вписанный), тогда дуга СТ = 54°
4) Проведем вписанный угол АДТ так, чтобы он был равен 90°, тогда дуга АТ = 180°
Дуга АС = 180° - 42° - 42° = 96°
Дуга АВ = 234° - 96° = 138°
5) Дуга ВQ = дуга ВАС + дуга QC = 234° + 42° = 276°
Дуга ДС = дуга ВАС + дуга ВД = 234° + 42° = 276°
Дуга АQ = дуга АВ + ВД + ДQ = 138° + 42° + 42° = 222°
Дуга АД = дуга АС + ДQ + QC = 96° + 42° + 42° = 180°
6) Угол ВАС = 63° (по условию)
Угол ДВА = 1/2 дуги АД (т.к. вписанный) = 180° : 2 = 90°
Угол ВДQ = 1/2 дуги ВQ = 276° : 2 = 138°
Угол ДQC = 1/2 дуги ДС = 276° : 2 = 138°
Угол QCA = 1/2 дуги AQ = 222° : 2 = 111°
ответ: Угол ВАС = 63°, угол ДВА = 90°, угол ВДQ = 138°, угол ДQC = 138°, угол QCA = 111°