Пусть стороны первого треугольника
а1=5 см; в1=6 см; с1=7 см.
Коэфф. подобия=к
Тогда стороны второго треугольника
а2=5к дм; в2=6к дм; с2=7к дм
По условию с2-а2=14
7к - 5к=14
2к=14
к=7
Отсюда а2=35 дм; в2=42 дм; с2=49 дм - это ответ.
Відповідь:
АВСМ - параллелограм
АВ || СМ
АВ = 2 см.
ВС = 3 см.
Пояснення:
Основания трапеции ВС и АД - параллельны. Пусть угол ВАМ = х, тогда и угол ВСМ = х. Из параллельности оснований трапеций следует, что в четырехугольнике АВСМ сумма углов ВАМ и АВС равна 180° и сумма углов ВСМ и АМС равна 180°. Значит
АВС = 180 - ВАМ = 180 - х
АМС = 180 - ВСМ = 180 -х
Следовательно углы ВАМ и ВСМ равны. Если в четырехугольнике АВСМ накрест лежащие углы равны то АВСМ - параллелограм.
У параллелограмма противолежащие стороны параллельны и равны.
Значит АВ || СМ.
АВ = СМ = 2 см.
ВС = АМ = 3 см.
Для доказательства достаточно показать, что один из углов, например, угол С прямой. Тогда все углы параллелограмма будут прямыми и получится прямоугольник.
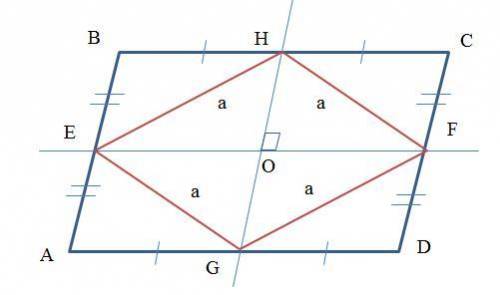
Пусть E, F, G и H середины сторон параллелограмма (см. рисунок).
Через пару точек E и F, G и H проведём прямые. Так как точки E и F, G и H середины сторон параллелограмма, то прямые EF || BC и GH || CD.
С другой стороны отрезки EF и GH являются диагоналями ромба EHFG и поэтому пересекаются под прямым углом, то есть EF⊥GH. Но EF || BC и GH || CD, откуда следует, что BC⊥CD, что и требовалось доказать.
Відповідь: 35, 42, 49 дм
Пояснення: фото