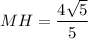
Объяснение:
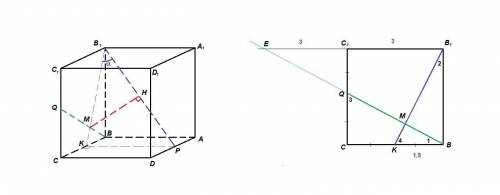
а) Проведем РК║АВ.
РК⊥(ВВ₁С₁), значит В₁К - проекция прямой В₁Р на плоскость (ВВ₁С₁).
ΔВ₁ВК = ΔBCQ по двум катетам, значит
∠1 = ∠2 и ∠3 = ∠4.
∠1 + ∠3 = 90°, значит в ΔКВМ ∠1 + ∠4 = 90°, следовательно,
∠ВМК = 90°, т.е. В₁К⊥BQ.
Но тогда и B₁P⊥BQ по теореме о трех перпендикулярах.
б)
РК⊥(ВВ₁С₁), значит РК⊥BQ,
BQ⊥B₁K (доказано в п. а), тогда BQ⊥(В₁КР).
Проведем МН⊥В₁Р в треугольнике В₁КР.
Так как МН⊂(В₁КР), то МН⊥BQ и МН⊥В₁Р по построению, тогда
МН - искомое расстояние между прямыми B₁P и BQ.
На выносном рисунке:
ΔВСQ = ΔEC₁Q по катету и острому углу (CQ = C₁Q и углы при вершине Q равны как вертикальные), ⇒ ЕС₁ = ВС = 3.
ΔВ₁МЕ ~ ΔKMB по двум углам (при вершине М - вертикальные и ∠1 = ∠Е как накрест лежащие при ВС║В₁Е и секущей ВЕ):
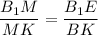
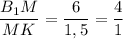 ⇒
⇒
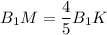
Из прямоугольного треугольника В₁ВК по теореме Пифагора:
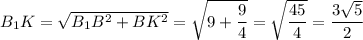
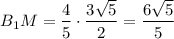
Из прямоугольного треугольника В₁КР по теореме Пифагора:
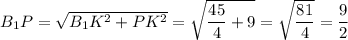
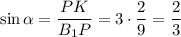
ΔB₁MH:
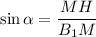
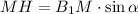
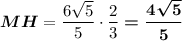
EF - средняя линия
EO = 3 см
OF = 4 см
Найти: AB
Решение.
1) Рассмотрим трапецию ABCD. Средняя линия EF параллельна основаниям AB и DC и делит стороны AD и BC трапеции пополам.
2) Рассмотрим треугольники EOD и ABD.
Углы EOD и ABD равны как соответственные при пересечении параллельных прямых EF и AB секущей BD.
Угол DBC общий. Следовательно, треугольник BOF подобен BDC.
3) Из подобия треугольников следует, что
AB / EO = AD / ED => AB = EO * AD / ED = EO * 2ED / ED = EO * 2 = 6 см.