Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
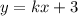
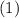
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы 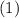выразим k:
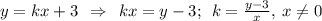
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)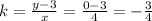 
В итоге, формула линейной функции получится следующей:
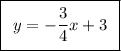
1) Для любого многоугольника, описанног около окружности
S =r*p, где р - полупериметр.
Тогда периметр 2p = 2S/r =2*13/1 = 26.
2) Треугольник равнобедренный, высота СН делит сторону АВ пополам.
Обозначим СН за "х", а АН за "у".
tgA = x/y = 9/40 40x = 9y x = 9y/40
По Пифагору x^2 + y^2 = 8,2^2 = (8(1/5))^2 = (41/5)^2 = 1681/25
Подставив x = 9y/40 в это уравнение, получим
(81y^2)/1600 + y^2 = 1681/25
y^2 = 64 y = 8
Высота CH= х = 9*8/40 = 9/5