По определению тангенса: Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему
значит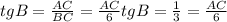 
Отсюда найдем AC
AC=2,
Далее по теореме Пифагора найдем гипотенузу AB
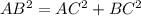
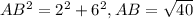
Получим,что AB=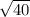
, AC=2
Если често,то что-то я не уверена в правильности своего решения,в геометрии меня всегда смущали ответы в виде квадратного корня ,хотя в большинстве случаев это оказывалось правильно.
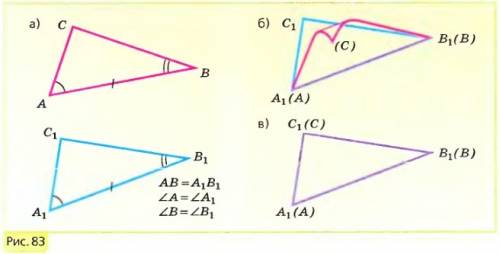
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, ∠A = ∠A1, ∠B = ∠B1 (рис. 83, а), и докажем, что эти треугольники равны.
Мысленно наложим треугольник ABC так, чтобы вершина A совместилась с вершиной A1, сторона AB – с равной ей стороной A1B1, а вершина C и C1 оказались по одну сторону от прямой A1B1 (рис. 83, б).
Так как ∠A = ∠A1 и ∠B = ∠B1, то сторона AC наложится на луч A1C1, а сторона BC – на луч B1C1. Поэтому вершина C – общая точка сторон AC и BC – совместится с общей точкой лучей A1C1 и B1C1, т. е. с точкой C1 (рис. 83, в). Из этого следует, что стороны AC и BC совместятся соответственно со сторонами A1C1 и B1C1. Итак, треугольники полностью совместятся, и, следовательно, они равны. Теорема доказана.
tgB=AC/BC=1/3
AC=6:3=2
AC^2=6^2+2^2=40
AC=√40