
1. Прямая ВC формула прямой у=(3-х)/7
Прямая АВ формула прямой у=2х-21
Прямая АС формула прямой у= -х-3
2. у=9-3х медиана АА1
у=1/3х-39/9 - медиана ВВ1
у= -0,5х-1 - медиана СС1
3. у(АА2)=7,1х-51,5
ВВ2 высота у=х-11
СС2 уравнение у= -0,5х-1
4. А3(5;-6) т пересечения медианы АА1 и высоты ВВ2
5.tg∠A=3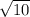
tg∠B=tg∠A
tg∠C=2/3/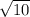
Объяснение:
1. Коэфициент при х - это (у-уо)/х т.В(10;-1)
для ВС (у-уо)/х=(-1+21)/10=2
2. АА1 - медиана Определим координаты А1(3; 0)
уравнение медианы АА1
у=9-3х
ВВ1 - медиана В1(1; -4)
у=1/3х-39/9
СС1 С1 (8; -5)
у= -0,5х-1
3.АА2 высота
А2 (7,2; -0,6)
у(АА2)=8,5/1,2х-61,8/1,2=7,1х-51,5
ВВ2 высота
координата В2=(4; -7)
у=х-11
СС2 тС2=С1 (8; -5)
у= -0,5х-1
5. tg∠A=CC1/AC1
Определяем модули векторов СС1 (12;-6) и АС1 (2;4)
tg∠A= /
/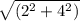 =3
=3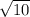
tg∠B=tg∠A
tg∠C=2*AC1/CC1=2*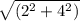 /
/ =2/3/
=2/3/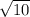
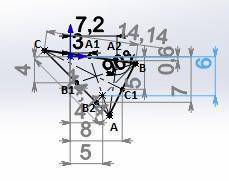
№1
Углы 2 и 5 смежные, их сумма равна 180°. Значит, ∠5=180-133=47°.
Углы 1 и 5 соответственные при прямых a и b и секущей c, ∠1=47° и ∠5=47°, ⇒ a||b (по признаку параллельных прямых: если соответственные углы равны, то прямые параллельны) ч.т.д.
№2
Так как по условию BM=MK, то △BMK - равнобедренный. В равнобедренном треугольнике углы при основании равны, значит ∠KBM=∠BKM.
Так как по условию BK - биссектриса △ABC, то ∠ABK=∠KBC=∠KBM.
Итак, ∠KBM=∠BKM и ∠ABK=∠KBM. Значит, ∠ABK=∠BKM, при этом ∠ABK и ∠BKM - внутренние накрест лежащие углы при прямых AB и KM и секущей BK, ⇒ KM||AB, (по признаку параллельных прямых: если внутренние накрест лежащие углы равны, то прямые параллельны) ч.т.д.
№3
Так как по условию ∠BCE=80° и CK - биссектриса ∠BCE, то ∠KCE=∠BCE:2=80°:2=40°.
∠BAC=40° (по условию) и ∠KCE=40°, при этом ∠BAC и ∠KCE - соответственные углы при прямых AB и СK и секущей AE, ⇒ AB || СK (по признаку параллельных прямых: если соответственные углы равны, то прямые параллельны) ч.т.д. .