В условии ошибка. Если сторона квадрата 24, то его диагональ 24√2 ≈ 34. Тогда в треугольнике ASC сторона АС больше суммы двух других сторон: 34 > 13 + 13, т.е. треугольник с такими сторонами не существует.
Встречается такая же задача с другими данными:
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Пирамида правильная, значит в основании лежит квадрат, а боковые грани - равные равнобедренные треугольники.
Проведем SH⊥CD. Тогда CH = HD (треугольник SCD равнобедренный).
CH = HD = 1/2 CD = 5.
ΔSCH: ∠SHC = 90°, по теореме Пифагора:
SH = √(SC² - CH²) = √(169 - 25) = √144 = 12
Sпов = Sосн + Sбок
Sосн = AD² = 10² = 100
Sбок = 1/2 Pосн · SH = 1/2 · 10 · 4 · 12 = 240
Sпов = 100 + 240 = 340 ед. кв.
В треугольнике АВС точки М и Р середины сторон АВ и ВС соответственно. Найдите координаты точки С ,если А(0;2), М (3;5) Р (7;4). Решите задачу
Объяснение:
Пусть РК║АВ , тогда К -середина АС , по т. Фалеса. АМРК-параллелограмм по определению.Вектор МА(0-3;2-5) или МА(-3 ;-3) *****Пояснение-Точка А получена параллельным переносом точки М на вектор МА . И точка К может быть получена точно таким же параллельным переносом точки Р в точку К параллельным переносом на вектор МА . *****
х(К)=х(Р)+х(МА) ⇒ х(К)=7+(-3)=4,у(К)=у(Р)+у(МА) ⇒ х(К)=4+(-3)=1 . Значит точка К(4; 1).
Для отрезка АС точка К-середина. По формулам середины отрезка ищем координаты точки С :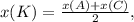 х(С)=2*х(К)-х(А) или х(С)=8-0=8 . Аналогично у(С)=2-2=0 . Поэтому С(8;0).
х(С)=2*х(К)-х(А) или х(С)=8-0=8 . Аналогично у(С)=2-2=0 . Поэтому С(8;0).
Для отрезка ВС точка Р-середина. По формулам середины отрезка ищем координаты точки Р :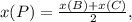 х(С)=2*х(Р)-х(В) или х(С)=14-6=8 . Аналогично у(С)=8-8=0 . Поэтому С(8;0)
х(С)=2*х(Р)-х(В) или х(С)=14-6=8 . Аналогично у(С)=8-8=0 . Поэтому С(8;0)