 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 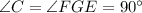 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 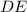 , то
, то 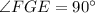 ).
).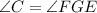 и
и 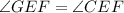 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: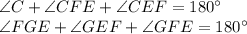
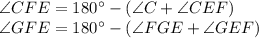
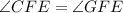 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: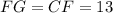
 . Смотрите второй рисунок.
. Смотрите второй рисунок.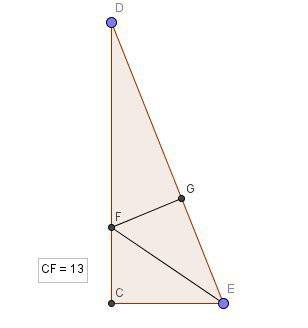
Назовем треугольник АВС.
Если провести перпендикуляр ВН, образуется два треугольникаАВН и ВНС. В равностороннем тр все стороны равны и углы по 60градусов. Тогда в одном из образовавшихся треугольников видим, что поделенное основание( половина его) равно половине гипотенузы, потому что сторона, лежащая напротив угла в тридцать градусов равна половине гипотенузы. Поэтому АН равен половине АВ, он лежит напротив угла АВН=30гр.
АН=х АВ=2х
Запишем уравнение:
По теореме Пифагора найдем х: x^2+12^2=(2x)^2
48=x^2
x=корень из48
сторона будет равна 2корня из 48, потому что АН=НС, высота поделила сторону напополам!
АС=АВ=ВС=2корень из48
S= 12*2корень из48/2= 12корень из48. одного треугольника.
Чтобы найти площадь треугольника, образованного сторонами-мелианами, нарисуем треугольник побольше, его стороны будут лежать за пределами маленького треугольника и в центрах высот углов маленького треугольника. Данная фигура образует 4 одинаковых треугольника, поэтому площадь фигуры равна:
Площадь всей фигуры равна 4*s
=4*12корень из48=48корень из48. ответ:48корней из 48.