Рисунок к задаче простой, каждый сумеет нарисовать прямоугольный треугольник.
Нарисуем треугольник АВС, проведем высоту СН.
Обратим внимание на то, что в треугольнике АВС, так как СН перпендикулярно АВ,
косинус А можно выразить не только, как АС:АВ, но и АН:АС
Тогда из соs A=√51):10 получим отношение
АН:АС=√51):10
Произведение крайних членов пропорции равно произведению ее средних членов:
10 АН=12√51
АН=12√51):10
По т.Пифагора из треугольника АСН
СН²=АС²-АН²
СН²=144 -144·51:100
Приведем к общему знаменателю:
СН²=(144·100 -144·51):100
СН²=144(100-51):100
СН²=144·49:100
СН=12·7:10=84:10=8,4
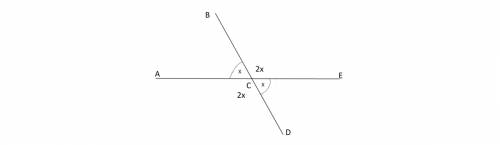
Сделаем простой рисунок и рассмотрим его.
Сумма углов, получающихся при пересечении двух прямых, равна 360 градусов.
Для угла АСВ смежными являются углы ВСЕ и АСD
Из условия задачи известно, что
∠ВСЕ+∠ACD=4∠АСВ
Cумма смежных с углом АСВ углов равна
∠ВСЕ+∠ACD=360° -∠АСВ-∠DCE
Но ∠АСВ=∠DCE как вертикальные углы.
Поэтому
∠ВСЕ+∠ACD=360-2∠АСВ
360° - 2∠АСВ=4∠АСВ
6∠АСВ=360°
∠АСВ=360°:6=60°
Сумма смежных с углом АСВ углов равна 60*4=240°
Проверим:
∠ВСЕ+∠ACD+АСВ+DCE=
240°+60°+60°=360°
----------
По какой-то причине знак угла в некоторых местах иногда выглядит прямоугольником. На результат решения это не влияет.
Что такое D, не очень понятно, поэтому найдем все стороны треугольника. Обозначим МВ = х; Тогда из теоремы косинусов
(2 + x)^2 = 5^2 + (3 + x)^2 - 2*5*(3 + x)*cos(60) = 5^2 + (3 + x)^2 - 5*(3 + x);
Это - даже не квадратное уравнение, его легко првести к виду
(3 + x)^2 - (2 + x)^2 = 5*х - 10;
5 + 2*x = 5*x - 10; x = 5;
Стороны треугольника 5, 7, 8.