Что и требовалось доказать!
Объяснение:
Теорема: "Если при пересечении двух прямых секущей односторонние углы в сумме составляют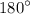 
, то прямые параллельны".
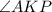и 
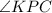- односторонние при пересечении прямых 
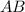и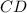 
секущей 
.
.
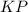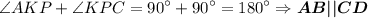Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Т.к.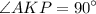 
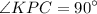
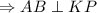и 
и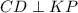 
.
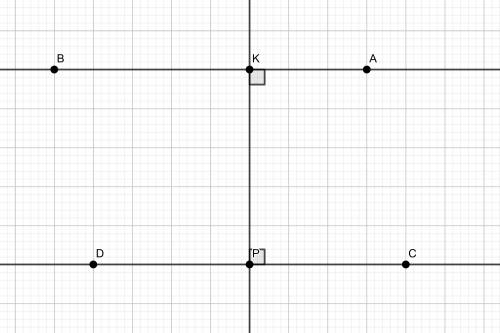
Признак: "Если две различные прямые на плоскости перпендикулярны к одной и той же прямой, то они параллельны".
Т.к. 
и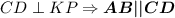 
.
Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
сначало ищем по тригонометрическому кругу(или по таблице) чему равен cosx=-1/2 cos=2п/3+2пn и cos=4п/3+2пn. потом выражения. после сортируем корни (я предпочитаю числовую прямую) вместо n подставляем целые числа и смотрим лежит ли данная точна на отрезке [-пи/2; 5пи/2]. ответ -п/3; п/3; 2п/3; 7п/3