ответ: 10 см.
Объяснение:
Пусть D(1) - диаметр окружности, величина которого равна 4 см; D(2) - диаметр окружности, величина которого равна 16 см; r(1) - радиус окружности, с диаметром D(1); r(2) - радиус окружности, с диаметром D(2).
D(1) = r(1) * 2 = 4 см ⇒ r(1) = D(1)/2 = 4/2 = 2 см.
D(2) = r(2) * 2 = 16 см ⇒ r(2) = D(2)/2 = 16/2 = 8 см.
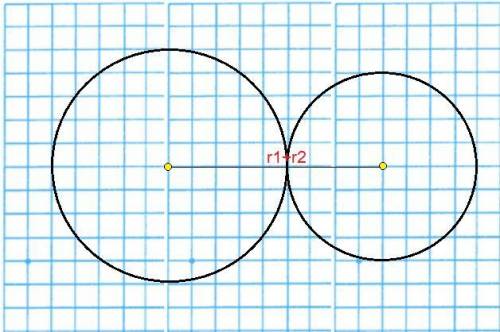
На рисунке изображено внешнее касание окружностей и можно увидеть, что расстояние между центрами окружностей равно сумме их радиусов.
Пусть d - расстояние между центрами окружностей.
⇒ d = r(1) + r(2) = 2 + 8 = 10 см.
Ясно, что сторона большого квадрата равна √49=7/см/, и если рассмотреть верхний левый треугольник, в котором гипотенуза АВ равна 5см, введя переменную х- пусть это будет меньший катет, тода больший катет равен (7-х),по теореме Пифагора
х²+(7-х)²=25; х²+х²-14х+49=25; 2х²-14х+24=0; х²-7х+12=0; По Виета х=3 или х=4, т.е. если один катет 3см, то второй 4см, и наоборот.
А это и есть стороны тех четырех прямоугольников, зная площадь одного, найдя площадь четырех и от площади квадрата отняв полученную площадь, найдем площадь маленького квадрата
Она равна 49-4*4*3=49-48=1/см²/
ответ 1см²
Периметром трикутника