Правильный треугольник ABC вписан в окружность с центром O и радиусом 8 см. На стороне этого треугольника построен квадрат. Определить радиус окружности, описанной около квадрата.
=======================================================
У правильного треугольника и квадрата общая сторона АВ ⇒ все стороны данных правильных многоугольников равны друг другуСторона правильного треугольника рассчитывается через радиус описанной окружности:а = r•√3Радиус окружности, описанной около квадрата, рассчитывается через сторону квадрата:R = a•√2/2 = (r•√3)•√2/2 = r•√6/2 = 8•√6/2 = 4√6ОТВЕТ: 4√6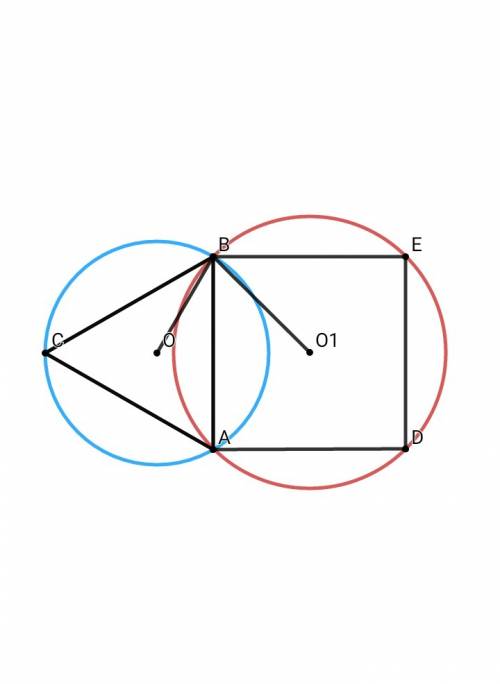
Для решения задачи нужна площадь треугольника.
Её можно тупо сосчитать по формуле Герона, а можно и сообразить, что треугольник "составлен" из двух Пифагоровых треугольников со сторонами (5,12,13) и (9,12,15), так, что катет 12 у них общий, а катеты 5 и 9 вместе составляют сторону 14 исходного треугольника.
То есть высота к стороне 14 равна 12.
Итак, площадь треугольника S = 14*12/2 = 84;
Полупериметр равен (13 + 14 + 15)/2 = 21;
Поэтому радиус вписанной окружности равен r = 84/21 = 4;
Сечение шара плоскостью треугольника как раз и дает нам круг, ограниченный вписанной окружностью. При этом радиус этой окружности r, расстояние d от центра до плоскости сечения (до плоскости треугольника) и радиус шара R связаны теоремой Пифагора.
R^2 = r^2 + d^2;
Отсюда d = 3; (тут Пифагорова тройка 3,4,5)
боковое ребро - b
высота пирамиды h=b*sin α
проекция b на плоскость основания b " = b* cos α
медиана основания m = 3/2 * b " = 3/2 * b* cos α
сторона основания a = m / sin60 = 3/2 * b* cos α / √3/2 =√3*b*cos α
площадь основания So = a^2 *sin60 = (√3)^2*b^2*cos^2 α *√3/2 = 3√3/2 *b^2*cos^2 α
объем пирамиды V = 1/3 *h*So = 1/3 *b*sin α *3√3/2 *b^2*cos^2 α =√3/2 *b^3*sin α*cos^2 α