18.16
Четырехугольник, у которого противоположные стороны попарно параллельны. называют параллелограммом. Если мы докажем равенство векторов, на которых лежат данные противоположные стороны, то задача будет решена. Но можно ограничиться и равенством длин векторов, на которых лежит две противоположные стороны. Тогда будет доказано, что две стороны параллельны и равны. и по признаку параллелограмма тоже будет доказано, что АВСD - параллелограмм.
Если векторы равны, то равны их модули и векторы сонаправлены.
18.16
1) Векторы имеют такие координаты АВ(-1;-1;4)= DС(-1;-1;4)
ВС(3;-3;-2)=АD(3;-3;-2)
2) АВ(-1;-1;4)=DС(-1;-1;4); ВС(-3;1;-2)=АD(-3;1;-2)
18.17. Если модули всех четырех векторов, на которых лежат стороны ромба, равны, то длины этих векторов равны и по признаку ромба этот четырехугольник является ромбом. Т.е. если стороны четырехугольника равны, то он является ромбом. Проверим. АВ(2;-5;-2) его длина √(4+25+4)=√33; ВС(-4;1;-4) его длина √(16+16+1)=√33; СD(-2;5;2), его длина √(4+25+4)=√33; AD(-4;1;-4) и его длина √(16+1+16)=√33 Доказано.
Аналогично 2) АВ(1;-2;0) длина√5; ВС(1;0;2) его длина √(1+4)=√5, СD(-1;2;0), его длина √(1+4+0)=√5; AD(1;0;2) и его длина √(1+0+4)=√5 Доказано.
/√3 ⇒ KO =CO/√3 =CO√3 /3= 4√6 /3 (см).
-------
KC =2*KO =8√6 /3
-------
Sпол = Sосн +
Дано:
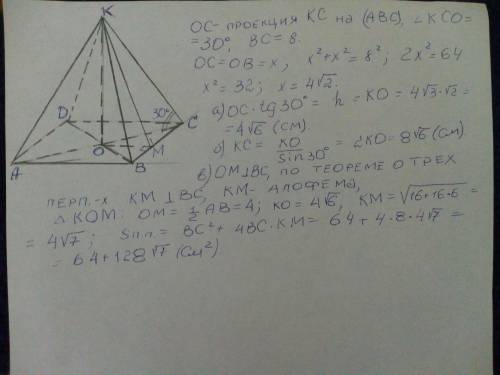
KABCD _правильная четырехугольная пирамида
(K_вершина , квадрат ABCD _основание
AB=BC=CD =DA = a =8 см ;
KO_ высота ; KO⊥ пл.(ABCD)
∡KCO = 30° ------------------------
а) KO = h - ? 4√6 /3 см .
б) KA = KB =KC =KD = b - ? 8√6 /3 см .
в) S пол - ? 64(3 +√15) / 3
AC =a√2 ; CO =AO = AC/2 =a√2 /2 = 8√2 / 2 = 4√2 ( см) .
В ΔKOC: KO = KC/2 (катет против угля 30°) ⇒ KC = 2*KO =2h
(2*h)²- h² =CO² ⇔ h = CO√3 /3 = 4√2√3 / 3 = 4√6 /3
KO = h= 4√6 /3 (см) .
KC = 2*KO = 8√6 / 3 (см)
-------
Sпол = Sосн + Sбок
Sосн = a² = 8² см² =64 см²
Sбок =4*S(ΔKCD) =4*a*KM/2 =2a*KM =16*KM
KM =√ (KC² -(a/2)²) =√( (8√6 /3)² - 4² ) =√( (64*6/9 - 16 ) =4√15 /3.
Sбок =64√15 / 3
Sпол =64 +64√15 / 3 = 64(3 +√15) / 3
ав=вс ам=мс сам=мас
мныкы дурыс апаи дан сурадым бырак дурыс болмаи калуы мумкын
Объяснение: