
вот
Объяснение:

S полн = 66
Объяснение:
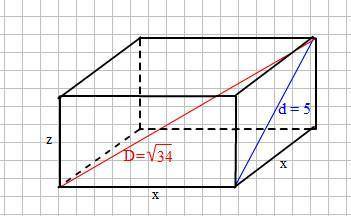
Смотри прикреплённый рисунок
х - ? - сторона квадрата, лежащего в основании призмы
z - ? - высота призмы
d = 5 - диагональ боковой грани
D = √34 - диагональ призмы
Найдём размерности параллелепипеда, который представляет собой призма.
Треугольник, составленный из D, d и х - прямоугольный с гипотенузой D, потому что d ⊥ x по теореме о трёх перпендикулярах.
х² + d² = D² ⇒ x² = D² - d² = 34 - 25 = 9 ⇒ x = 3
x² + x² + z² = D² ⇒ z² = D² - 2x² = 34 - 2 · 9 = 16 ⇒ z = 4
Площадь полной поверхности призмы равна
S полн = 2х² + 4x · z = 2 · 9 + 4 · 3 · 4 = 66
Пусть SO - высота пирамиды. МК пересекает SO в её середине (точка Р), поскольку является средней линией треугольника SAС.
Если через точку В провести прямую II AC и МК (одновременно - они между собой параллельны), то эта прямая будет принадлежать обеим плоскостям ВМК и АВС, будет перпендикулярна ВО и РО (РО вообще перпендикулярно плоскости АВС), а => и РВ. Поэтому искомый угол - это ОВР, обозначим его за Ф, ясно, что
tg(Ф) = РО/ВО. Вобщем-то, задача решена, так как РО = SO/2;
ВО = 6*корень(2)/2 = 3*корень(2); SO = корень(SB^2 - ВО^2) = корень(8^2 - (3*корень(2))^2) = корень(46); PO = корень(46)/2;
Какой-то тангенс получился кривой, и, как я не крутил, нормальных чисел не вышло.
Ну, tg(Ф) = корень(23)/6.
ответ:.......
Объяснение: