1) По теореме пар-амма противолежащие углы равны. Обозначим за х-меньший угол, за 2х больший. Два меньших угла- 2х, два больших 4х. Вместе они равны 360. Т.е.,
2х+4х=360
6х=360
х=360/6
х=60
ответ. 60
3) У равнобедренной трапеции углы при основании равны. Пусть меньший угол x, а больший 2х, т.к. относится как 1 к 2. Меньших углов два, значит 2x, и больших 2, значит 4x.
Вместе они 360.
Решаешь как в первое задаче уравнение и ответ тот же.
Вторую, извини, не могу
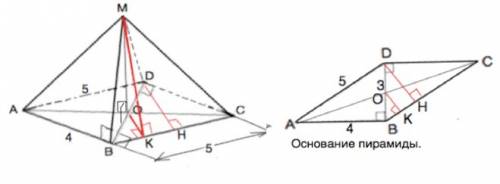
Площадь полной поверхности пирамиды (обозначим её МАВСD)
состоит из суммы площадей всех граней.
Противоположные боковые грани равны по трём сторонам.
Так как МО перпендикулярна плоскости основания, а ВD⊥АВ и CD, то ОВ – проекция наклонной МВ.
По т.о 3-х перпендикулярах МВ⊥АВ.
Диагонали параллелограмма точкой пересечения делятся пополам ⇒. ОВ=1,5.
Высота пирамиды МО⊥ОВ.
Из ∆ МОВ по т.Пифагора
МВ=√(МО²+ОВ²)=√(4+2,25)=2,5
Ѕ(АМВ)=МВ•АВ:2=2,5•4:2=5 м²
Ѕ(MCD)=S(AMB) ⇒Ѕ(MCD)+S(AMB)=10 м²
Найдём высоту второй пары боковых граней.
а) Высота DH прямоугольного ∆ BDH (в основании) равна произведению катетов, делённому на гипотенузу.
DH=DB•DC:BC=3•4:5=2,4 м
Проведем ОК⊥ВС
ВO=ОD ⇒ ОК - средняя линия ∆ВDH и равна половине DH.
ОК=1,2 м
ОК - проекция наклонной МК. ⇒ По т.ТПП отрезок МК⊥ВС и является высотой ∆ ВМС
б) Из прямоугольного ∆ МОК по т.Пифагора
МК=√(MO²+OK²)=√(4+1,44)=√5,44
√5,44=√(544/100)=(2√34):10=0,2√34
S(MBC)=BC•MK:2=0,5•5•0,2√34=0,5√34 м²
S(AMD)=S(MBC)⇒ S(AMD)+S(MBC)=2•0,5√34=√34 м²
S(ABCD)=DB•AB=3•4=12 м²
Площадь полной поверхности MABCD:
2•S(AMB)+S(ABCD)+2•S(MBC=10+12+√34=(22+√34)м²
1)Противоположные углы пар-мма равны, пусть меньший угол х градусов, значит больший угол 2х , составим уравнение..2х+4х=360, х = 60..меньший угол 60 градусов
3)
a/b=1/2
2a=b
a+2a=180
3a=180
a=60 4.t.d