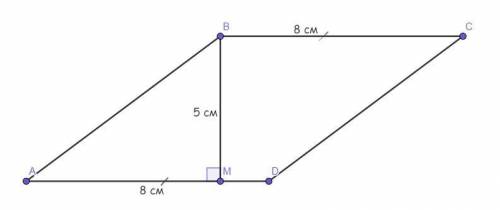
У параллелограмма ABCD проведена высота ВМ к стороне AD. Найдите площадь этого параллелограмма, если ВС = 8 см, ВМ = 5 см.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
Дано:Четырёхугольник ABCD — параллелограмм.
ВМ — высота, опущенная на сторону AD = 5 см.
ВС = 8 см.
Найти:S(ABCD) = ?
Решение:▸Противоположные стороны параллелограмма равны◂
AD и ВС — противоположные стороны.
Следовательно, по выше сказанному —
AD = ВС = 8 см.
▸Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону◂
Следовательно —
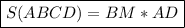
Подставим в формулу известные нам значения в формулу —
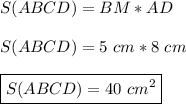ответ: 40 см².
Теорема.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.
Проведем через точку В2 прямую С1С2, параллельную прямой A1A2. Получаем параллелограммы A1C1BA2 и A2B2C2A3. По свойствам параллелограмма, A1A2 = C1B2 и A2A3 = B2C2. Так как A1A2 = A2A3, то C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3 по второму признаку равенства треугольников (C1B2 = B2C2, ∠ C1B2B1 = ∠ C2B2B3, как вертикальные, ∠ B1C1B2 = ∠ = B3C2B2, как внутренние накрест лежащие при прямых B1C1 и C2B3 и секущей С1С2). Из равенства треугольников следует, что B1B2=B2B3. Теорема доказана.