1. Пусть одна сторона параллелограмма равна х см, а вторая у см. Тогда периметр параллелограмма будет равен 2х+2у=48 см, но по условию известно что х-у=7 см.
Решим полученную систему уравнений:
2х+2у=48
х-у=7 |*2 (умножим второе уравнение на 2);
2х+2у=48 (сложим полученные уравнения)
+
2х-2у=14;
2х+2х+2у-2у=48+14
4х=62
х=62/4
х=15,5
Найдем у:
х-у=7
15,5-у=7
-у=7-15,5
у=8,5
ответ: Стороны параллелограмма равны 15,5 см и 8,5 см.
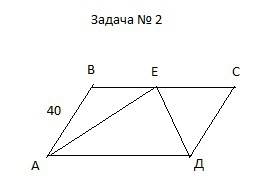
2. АВ=СД (так как АВСД – параллелограмм)
Свойство биссектрисы параллелограмма:
Биссектриса параллелограмма отсекает равнобедренный треугольник
Значит АВ=ВЕ=40 см. и СД=СЕ=40 см.
ВС=ВЕ+СЕ=40+40=80 см.
ADPT - квадрат
Объяснение:
Если MA=BD=CP=KT, то AB=DC=PK=TM, т.к. все стороны квадрата равны по определению.
Соединив точки A,D,P и T получим прямоугольные треугольники ABD, DCP, PKT и TMA с равными сторонами, т.е. и равные гипотенузы AD=DP=PT=TA, а именно равные стороны фигуры ADPT.
Построив две прямые, соединив точки D и T, а так же A и P, получим две прямоугольные трапеции ABCP и AMKP, с равными основаниями, вершинами и одной стороной, то и вторые стороны этих трапеций будут равны DT=AP.
Имея равные стороны AD=DP=PT=TA и равные диагонали DT=AP, получим квадрат ADPT.
ч.т.д.
V=1/3*пи*h*r в квадрате
V=1/3*20*144*пи=960пи