Найти: d
По основному тригонометрическому свойству:
cos²(BAO)+sin²(BAO)=1
(0,6)²+sin²(BAO)=1
sin²(BAO)=0,64
Совокупность:
sin(BAO)=0,8
sin(BAO)=–0,8
Так как угол ВАО меньше 180°, то sin(BAO)=0,8
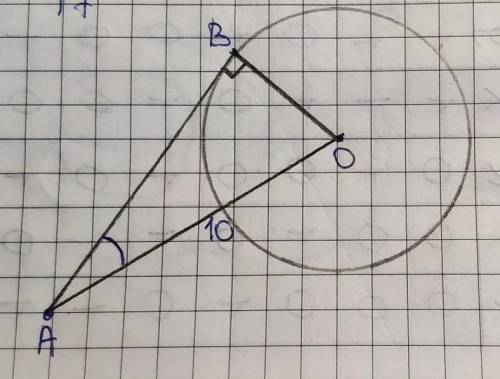
Проведем ОВ.
ОВ перпендикулярен АВ, так как радиус окружности, проведенный к точке касания касательной, перпендикулярен этой касательной.
То есть угол ОВА=90°, а ∆ОВА – прямоугольный.
В прямоугольном ∆ВАО:
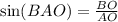
Подставим известные значения:
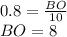
ВО – радиус окружности.
Диаметр вдвое больше радиуса, следовательно d=BO*2=8*2=16 см.
ответ: 16 см.
1) CB = AB = 8, AC = 8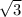
, <A = <C = 30 <B = 120
2) 400 * sin113 * sin53 / sin14
3) AC =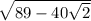 
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Объяснение:
1) <C = 180-120-30 = 30 значит треугольник ABC равнобедренный с основанием AC. CB = AB = 8. Пусть BD высота, она же медиана.
<DBA = 120 / 2 = 60. AD = AB * sin<DBA = 8* 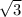/2 = 4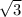
AC = 2AD = 8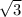
2) BC = AC * sinA / sinB
S = AC * BC * sinC / 2 = 20* 20 * sin113 * sin53 / sin14
3) AC = 
так как все стороный найдены можно подставить их значения в формулы:
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Можно выбрать такую систему единиц измерения длин, что сторона квадрата в нижнем основании усеченной пирамиды равна m, а в верхнем n;
Ясно, что высота пирамиды равна диаметру шара H = D;
Объем шара Vs = (4*π/3)*(D/2)^3 = (π/6)*D^3;
Объем усеченной пирамиды равен
V = (H/3)*(S1 + √(S1*S2) + S2) = (D/3)*(m^2 + m*n + n^2);
Vs/V = (π/2)*D^2/(m^2 + m*n + n^2);
то есть надо найти высоту пирамиды H = D.
Сечение, проходящее через точки касания шара с основаниями и противоположными боковыми гранями - это равнобедренная трапеция, в которую вписана окружность диаметра H. Её основания - это "средние линии" квадратов в основаниях, то есть они равны m и n.
По свойству описанных четырехугольников, суммы противоположных сторон равны, то есть боковая сторона этой трапеции равна (m + n)/2;
Если в этой трапеции из вершины меньшего основания опустить высоту, то она отсечет от большего основания отрезок (m - n)/2; (считая от ближайшей вершины, второй отрезок равен (m + n)/2; )
H^2 = ((m + n)/2)^2 - ((m - n)/2)^2 = m*n; осталось подставить.
Vs/V = (π/2)*(m*n)/(m^2 + m*n + n^2); это ответ.
если положить p = m/n; то
Vs/V = (π/2)*p/(p^2 + p + 1);