1)
Если трапеция равнобедренная, то АБ=СД=5, следовательно АБ+СД=10.
Тогда сумма двух оснований равна 32-10=22.
Площадь равна средняя линия * h(высоту)
Ср линия = 22/2=11.
Из формулы площади найдем высоту:
h=S/ср.лин
следовательно высота равна 44/11=4
ответ: h=4
2)
S(трапецииABCD) = (AD + BC) : 2 * h
h - высота трапеции и треугольника ACD
S(ACD) = 1/2 * AD * h, следовательно
h = S(ACD) / (1/2 * AD) = 30 / (1/2 * 10) = 30 : 5 = 6 см
S(трапецииABCD) = 1/2*(10 + 8) * 6 = 9 * 6 = 54 см²
P.S. 1/2 - 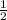
/ - дробь
Предположим, что тр-к ABC - равнобедренный
1) Проведём высоту AK к основанию BC. По св-ву равнобедр. тр., она будет также медианой и биссектрисой. Значит, тр-ки ABK b ACK будут равны по стороне и двум прилежащим углам (половины основания, углы при основании и два прямых угла).
2) Проведём высоты BM и CH к сторонам АС и АВ соответственно.
Три высоты пересекутсся в точке О, и все они будут делиться по соотношению 2:1, считая от вершин.
В 1 действии мы доказали, что тр. ABK и ACK равны. Значит, если высоты пересекаются в одной точке , лежащей на общей стороне AK этих двух треугольников, то отрезки высот - BO-OM и CO-OH будут равны (т.к. не смещена линия симметрии):
BO=CO
OM=OH
Если равны все отрезки высот, то буду равны и целые высоты:
BM = CH, чтд.
Всё!