Теорема о неравенстве треугольника звучит следующим образом:
каждая сторона треугольника меньше суммы двух других сторон.Соответственно подходит вариант 1) вместо углов должно быть сторон.
ответ: 1).→ Задача №4.Применим теорему о неравенстве треугольника. Для этого нужно сравнить каждую сторону с суммой двух оставшихся сторон.
Треугольник №1:
8 см, 2 см, 9 см.
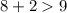- верно.
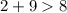- верно.
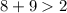- верно.Значит такой треугольник существует.
Треугольник №2:
18 см, 12 см, 14 см.
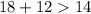- верно.
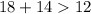- верно.
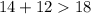- верно.Значит такой треугольник существует.
Треугольник №3:
110 см, 100 см, 90 см.
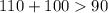- верно.
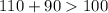- верно.
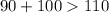- верно.Значит такой треугольник существует.
Треугольник №4:
3 см, 3 см, 7 см.
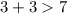- неверно.
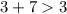- верно.
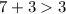- верно.Поскольку в первом случае сумма двух сторон меньше другой стороны, то такого треугольника не существует.
Треугольник №5:
79 см, 40 см, 40 см.
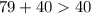- верно.
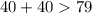- верно.
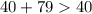- верно.Значит такой треугольник существует.
ответ: 4).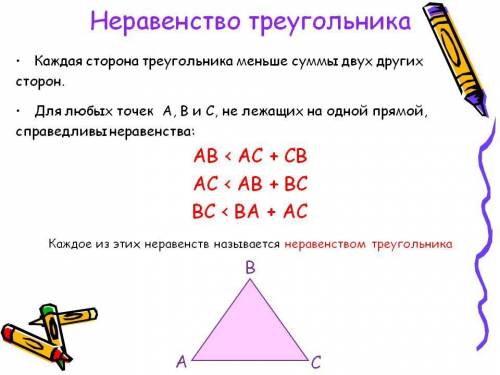
---------
Диагональ ВD делит трапецию на два прямоугольных треугольника.
Сумма острых углов АВСD равна 90º ⇒
∠ВАD+∠ВСD=90º
В прямоугольном ∆ АВD
∠ВАD+∠АВD=90º ⇒
∠АВD= ∠ВСD ⇒
прямоугольные ∆ АВD и ∆ ВСD подобны по равному острому углу.
Из подобия треугольников следует отношение:
АD:ВD=ВD:ВС
ВD²=АD*ВС=18*2=36
ВD=6
ВD- высота трапеции
S=BD*(AD+BC):2
S=6*(18+2):2=60 (ед. площади)