1) Как называются оси координат и точка их пересечения? 2) Какая плоскость называется координатной плоскостью ? Что такое координаты точки на координатной плоскости ?
мне нужно

👇

Ответ:

mam1975

05.03.2023

1) Ось абсцисс (ОХ), ось ординат (ОY). Точка пересечения - О с координатами 0;0 называется началом координат

2) Та плоскость, на которой лежат оси координат. Координаты точки - это два числа (абсцисса и ордината), которые обозначают точку на координатной плоскости.

4,6(55 оценок)

Открыть все ответы

Ответ:

geekeuphoria

05.03.2023

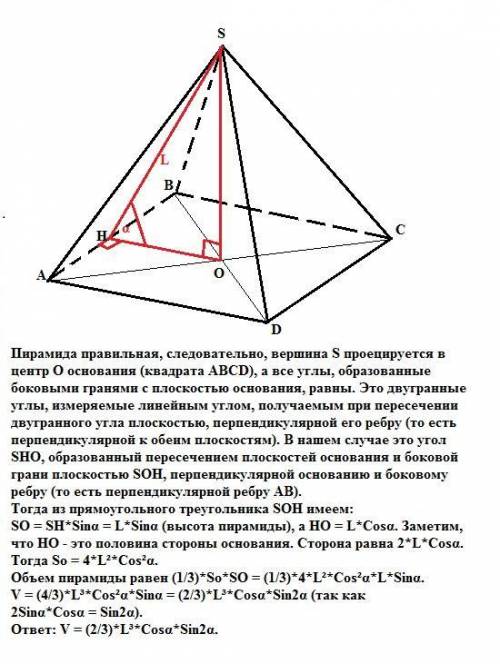
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).

Тогда из прямоугольного треугольника SOH имеем:

SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.

Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.

Тогда площадь основания So = 4*L²*Соs²α.

Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.

V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как

2Sinα*Cosα = Sin2α).

ответ: V = (2/3)*L³*Соsα*Sin2α.

Найдите объем правильной четырехугольной пирамиды,если ее апофема равна l ,а боковая грань образует

4,5(74 оценок)

Ответ:

Петя1134

05.03.2023

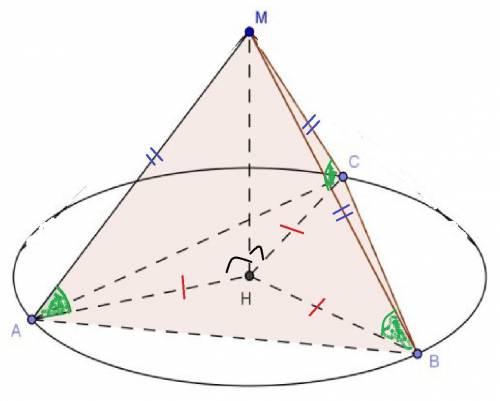
Если боковые рёбра равны, то вершины проецируется в центр описанной окружности (Это следует из равенства 3 треугольников по общему катету-высота пирамиды и гипотенузе-боковому ребру пирамиды). Тогда боковое ребро можно найти по теореме пифагора, где ребро - гипотенуза, радиус описанной окружности и высота пирамиды - катеты.

Для треугольника: 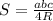$S=\frac{abc}{4R}$

Где a,b,c - стороны; R-радиус описанной; S-площадь.

А площадь можно найти через формулу Герона.

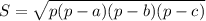
$S=\sqrt{p(p-a)(p-b)(p-c)}$

Где a,b,c-стороны треугольника; S-его площадь; p-полупериметр (половина от периметра).

А боковой ребро мы найдём: 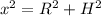x^2=R^2+H^2

Где x-боковое ребро; R-радиус описанной; H-высота пирамиды.

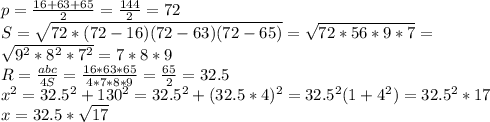
$p=\frac{16+63+65}{2}=\frac{144}{2}=72\\S=\sqrt{72*(72-16)(72-63)(72-65)}=\sqrt{72*56*9*7}=\\\sqrt{9^2*8^2*7^2}=7*8*9\\R=\frac{abc}{4S}=\frac{16*63*65}{4*7*8*9}=\frac{65}{2}=32.5\\x^2=32.5^2+130^2=32.5^2+(32.5*4)^2=32.5^2(1+4^2)=32.5^2*17\\x=32.5*\sqrt{17}$