1/12(а³×tgα×tgβ/cosα)
Объяснение:
АВС - треугольник, лежащий в основании пирамиды АВСD.
D - вершина пирамиды. ∠С=90°; ∠А=α; а - длина стороны АС; β - угол наклона боковых ребер к основанию.
Решение.
1. Опускаем из вершины D перпендикуляр на основание - это высота пирамиды DH. точка H - центр окружности, описанной около треугольника ABC, а т.к. этот треугольник прямоугольный, то H - середина гипотенузы AB. Тогда АН=0,5×АВ.
3. Находим длину катета ВС и гипотенузы АВ.
ВС=АС×tgα=a×tgα; AB=AC/cosα = a/cosα
3. Находим высоту пирамиды DH=AH×tgβ = 0,5×tgβ×a/cosα
4. Находим площадь основания
S = 0.5×AC×BC = 0.5×a×a×tgα = 0.5×a²×tgα
5. Рассчитываем объем пирамиды (0.5=1/2)
V = 1/3×(S×DH) = 1/3×(0.5×a²×tgα × 0,5×tgβ×a/cosα) = 1/12(а³×tgα×tgβ/cosα)
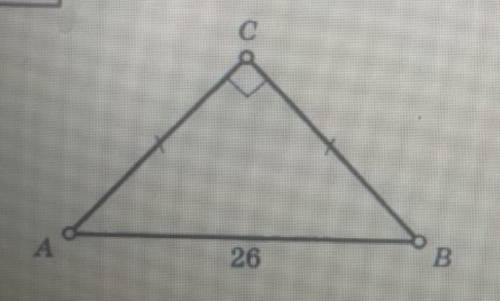
169
Объяснение:
1.проводим высоту из угла С, назовем ее СН
2. т.к.АВС равнобедренный, то СН- биссектриса, медиана, следовательно АСН=45°; АН=НВ=13
3. Т. АСН- прямоугольный, следовательно уг.САН=90-45=45°(сумма острых углов)=>т.АСН- равнобедренный,=>АН=НС=13
4.S=1/2AB*CH=1/2*26*13=169