
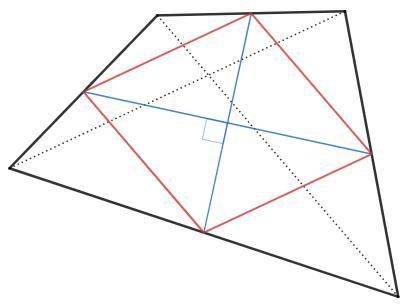
Соединим середины сторон четырехугольника.
Полученные отрезки параллельны диагоналям и равны их половинам, так как являются средними линиями в соответствующих треугольниках.
Отрезки образуют параллелограмм Вариньона.
Площадь четырехугольника Sч =1/2 d₁d₂ sinф
Угол ф между диагоналями четырехугольника равен углу между сторонами пар-ма Вариньона (т.к. они параллельны).
Площадь пар-ма Вариньона Sв =d₁/2 *d₂/2 *sinф =1/2 Sч
Итак, площадь пар-ма Вариньона равна половине площади четырехугольника.
В данном четырехугольнике диагонали равны, следовательно стороны пар-ма Вариньона равны и он является ромбом.
Диагонали ромба перпендикулярны, sin90=1.
Sч =2 Sв =2 *1/2 *14*8 =112
2одну
3 часть прямой с двух сторон ограниченная точками
4часть прямой ограниченная с одной стороны точкой. Либо двумя большими буквами, либо одной маленькой
5два луча исходящие из одной точки. вершина их общее начало, сторона это сами лучи
6обе его стороны лежат на одной прямой
7имеют одинаковую форму и размеры
8 наложить один на другой, чтобы один конец совпал с другим
9 делит его пополам
10 наложить, чтобы одна сторона совмеситлась с другой, а остальные в одну сторону
11 делит угол пополам
12сложить их
13линейка
14сколько градусов он содержит
15сложить их
16меньше 90°, равен 90°, больше 90 но меньше 180°
17хз
18 имеют одну общую сторону,180
19 в точке пересечения образуются прямые углы
20 прямые могут пересечься только в одной точке
21экер,теодолит