Точки M и N лежат на сторонах соотв. AB и AD пар-ма ABCD, причём AM/MB=1/2; AN/ND=3/2. DM пересекается с CN в точке K. Найдите отношения: DK/KM; CK/KN.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то треугольники подобны.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ . Доказать: ΔАВС подобен ΔА₁В₁С₁. Доказательство: Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) . Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках: АВ₂ : А₁В₁ = АС : А₁С₁. Сравним полученную пропорцию с данной в условии: АВ : А₁В₁ = АС : А₁С₁ Значит, АВ₂ = АВ. Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию). Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит ΔАВС подобен ΔА₁В₁С₁. Доказано.
Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)=
, x(K₁)=-3*2-0=-6,
y(A)=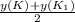
, y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.