Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 = . Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
а) Векторы ВВ1 и В1С совпадают с катетом и гипотенузой прямоугольного треугольника BВ1С, следовательно, ВВ1С=45°.б) BD = B1D1 , т.к. они сонаправлены и имеют одинаковую длину. BD = B1D1 =- DB .Угол между DB и DA — угол между стороной и диагональю квадрата, т.е. α=45°. Тогда угол междуDA и B1D1 равен 135°.в) A1C1 и A1B совпадают со сторонами равностороннего треугольника АВС и отложены из одной точки. Следовательно, угол 60°.г)(угол между стороной и диагональюквадрата).д)е)Пусть О — точка пересечения диагоналей В1С и ВС1,квадрата ВВ1С1С.следовательно,ж)следовательно,з)следовательно, угол между ними равен 180°Не знаете как решить? Можете с решением? Заходите и спрашивайте.
Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =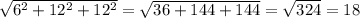
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 =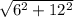 . Можно не считать, а пока оставить так.
. Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
d2 =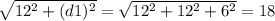
Отсюда и вытекает свойство о трёх измерениях.
ОТВЕТ: 18